Понятие энтропии

Для идеальной машины Карно справедливо, что

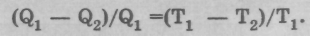
Отсюда получается равенство

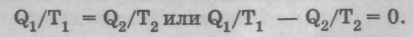
Так как количество теплоты Q₂ отдается холодильни­ку, его надо взять со знаком «минус». Следовательно, по­лучаем выражение

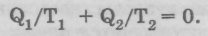
Будем писать вместо Q, подчеркивая, что речь идет о порции 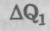, полученной рабочим телом от нагревате­ля, и порции 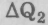, потерянной им в холодильнике.

Полученное выражение напоминает закон сохранения, а это, в свою очередь, не может не привлечь внимания к величине

В 1865 году Клаузиус ввел новое понятие «энтропия» (entropia — от греч. «поворот», «превращение»). Клаузис посчитал, что существует некоторая величина S, которая, подобно энергии, давлению, температуре, характеризует со­стояние газа. Когда к газу подводится некоторое количе­ство теплоты , то энтропия S возрастает на величину, равную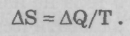

В предыдущей главе говорилось о том, что в течение длительного времени ученые не делали различий между такими понятиями, как температура и теплота. Однако ряд явлений указывал на то, что эти понятия следует раз­личать. Так, при таянии льда теплота расходуется, а тем­пература льда не изменяется в процессе плавления. После введения Клаузиусом понятия энтропии стало понятно, где пролегает граница четкого различения таких понятий, как теплота и температура. Дело в том, что нельзя говорить о каком-то количестве теплоты, заключенном в теле. Это понятие не имеет смысла. Теплота может передаваться от тела к телу, переходить в работу, возникать при трении, но при этом она не является сохраняющейся величиной. Поэтому теплота определяется в физике не как вид энер­гии, а как мера изменения энергии. В то же время введен­ная Клаузиусом энтропия оказалась величиной, сохраняю­щейся в обратимых процессах. Это означает, что энтропия системы может рассматриваться как функция состояния системы, ибо изменение ее не зависит от вида процесса, а определяется только начальным и конечным состояния-

ми системы. Покажем, что в идеальном цикле Карно эн­тропия сохраняется.

Рассмотрим величину , которая означает бесконеч­но малое приращение теплоты, настолько малое, что состо­яние системы характеризуется одним и тем же значени­ем температуры, неизменным по всему объему рассматри­ваемой системы. То есть предполагается, что система во все моменты времени находится в тепловом и механическом равновесии, и любое изменение ее состояния слагается из последовательности равновесных состояний, каждое из ко­торых лишь бесконечно мало отличается от предшеству­ющего. Именно такой характер поведения системы реали­зуется в обратимых процессах.

Если процесс обратимый, как в круговом цикле Карно, то

Из этого соотношения следует, что энтропия рабочего тела на 1-й стадии возрастает ровно настолько, насколь­ко она уменьшается на 3-й стадии. На 2-й и на 4-й ста­диях энтропия рабочего тела не изменяется, так как про­цессы здесь протекают адиабатически, без теплообмена.

Иными словами, в случае обратимых процессов,

то есть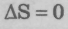

S = const — энтропия изолированной системы в случае обратимых процессов постоянна.

При необратимых процессах получаем закон возраста­ния энтропии: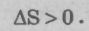

Для того чтобы осуществить обратимый процесс, необ­ходимо, как это уже упоминалось, добиться очень медленно­го расширения или сжатия рабочего тела, чтобы изменения системы представляли собой последовательность равновес­ных состояний. В таком цикле совершение какой-либо полезной работы потребует бесконечно большого времени. Чтобы получить работу в короткие промежутки времени, то есть хорошую мощность, приходится нарушать условия идеального цикла. А это сразу приведет к неодинаковос­ти температуры на разных участках системы, к потокам тепла от более горячих участков к менее горячим, то есть к возрастанию энтропии системы.

Для описания термодинамических процессов I начала термодинамики оказывается недостаточно, ибо I начало

термодинамики не позволяет определить направление про­текания процессов в природе. Тот факт, что энтропия изо лированной системы не может убывать, а только возрастает и достигает максимального значения в равновесном состо­янии, является отражением того, что в природе возможны процессы, протекающие только в одном направлении — в направлении передачи тепла только от более горячих тел менее горячим.

Существуют различные формулировки II начала термо­динамики. Все они являются эквивалентными. Приведем некоторые из них:

1. Невозможны такие процессы, единственным конеч­
ным результатом которых был бы переход тепла от
тела, менее нагретого, к телу, более нагретому.

В природе возможны процессы, протекающие только в одном направлении — в направлении передачи тепла только от более горячих тел менее горячим.

2. КПД любой тепловой машины всегда меньше 100
%, то есть невозможен вечный двигатель (перпетуум-мо­
биле) II рода (так как невозможно построить тепловую
машину, работающую не за счет перепада теплоты, а за
счет теплоты одного нагревателя).

КПД любой реальной тепловой машины всегда мень­ше КПД идеальной тепловой машины.

3. Энтропия изолированной системы при протекании
необратимых процессов возрастает, ибо система, предо­
ставленная самой себе, переходит из менее вероятного со­
стояния в более вероятное. Энтропия системы, находя­
щейся в равновесном состоянии, максимальна и постоян­
на

Эту последнюю формулировку требуется обсудить более подробно.

Дата добавления: 2015-05-07