
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретические сведения. Для описания изменяющейся позы тела каждый суставной угол следует представить в виде функций времени
|
|
|
|
Для описания изменяющейся позы тела каждый суставной угол следует представить в виде функций времени, вид которой зависит от характера суставного движения. В частности, при выполнении однократных (ациклических) движений для записи изменяющегося суставного угла может быть использована функция линейного характера:
φ  = φ
= φ 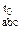 + (ω
+ (ω 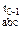 )t, (3.2.1)
)t, (3.2.1)
где: φ  – величина угла в суставе «b» цепи «а» для суставного движения типа «с» в некоторый момент времени «t»; φ
– величина угла в суставе «b» цепи «а» для суставного движения типа «с» в некоторый момент времени «t»; φ 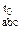 – величина угла в указанном выше суставе в начальный момент времени «t0»; ω
– величина угла в указанном выше суставе в начальный момент времени «t0»; ω 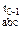 – средняя угловая скорость суставного движения для промежутка времени от t0 до t1.
– средняя угловая скорость суставного движения для промежутка времени от t0 до t1.
Более точным является гармоническое приближение, при использовании которого применяются периодические функции (sin и cos), выражающие зависимость суставного угла от времени.
Запись суставного угла в виде линейной функции времени, представленной выражением (3.2.1), называется линейным приближением. На рис. 3.2.1 представлен график изменения угла такого ациклического суставного движения. Такое приближение используется для записи переменной позы в настоящей лабораторной работе и для его записи необходимо знать величину изменения каждого угла и время, за которое произошло указанное изменение.
Для описания изменения позы тела в целом при выполнении сложных спортивных движений используют матричную форму записи, изложенную в лабораторной работе 3.1.
Рассмотрим несколько примеров описания изменений позы тела при выполнении ациклических суставных движений.
Пример 1. Спортсмен, находясь в положении основной стойки, за промежуток времени t2 – t1 = 0,2 с, поднимает руки вперед с некоторой средней угловой скоростью.
Позы тела для моментов времени t1 и t2 описываются следующим образом:
φ  = 0, φ
= 0, φ  ≠ 0
≠ 0
| 0 0 0 0 | t | 0 0 0 0 | t | |
| 0 0 0 0 | 0 0 0 0 | |||
φ  = =
| 0 0 0 0 | = 0, φ  = =
| 90 0 0 0 | (3.2.2) |
| 0 0 0 0 | 90 0 0 0 | |||
| 0 0 0 0 | 0 0 0 0 | 2. |
Первая строка представляет собой матрицы (в свернутом виде), определяющие плоскость выполнения сгибательно-разгибательных движений, а приведенные ниже развернутые матрицы – непосредственно суставные углы, образованные при выполнении указанных движений.
Величины изменений углов в суставах тела можно узнать, рассчитав разность между матрицами φ  и φ
и φ 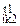 : *
: *
| 0 0 0 0 | t 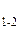 ** **
| |
| 0 0 0 0 | ||
φ  – φ – φ 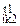 = =
| 90 0 0 0 | (3.2.3) |
| 90 0 0 0 | ||
| 0 0 0 0 | 1. |
Так как углы в плечевых суставах обеих рук за указанный промежуток времени изменились соответственно на –90 и 90, определим угловые скорости в плечевых суставах, пользуясь формулами (3.2.1):
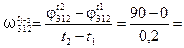
 ,
,
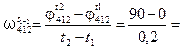 450 град/с.
450 град/с.
С учетом полученных величин в промежутке между моментами времени t1 и t2 изменение позы тела спортсмена описывается следующим образом:
φ 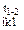 = 0,
= 0,
φ 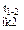 = φ
= φ  + φ
+ φ 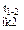 × t =
× t =
| 0 0 0 0 | t1-2 | |
| 0 0 0 0 | ||
| = 0 + | 450 0 0 0 | * t (3.2.4) |
| 450 0 0 0 | ||
| 0 0 0 0 |
Пример 2. Спортсмен в ходе физического упражнения в момент времени
t1 = 0 имел позу, изображенную на рис. 3.2.2а. Через 0,2с в момент времени t2 – позу, представленную на рис. 3.2.2б. Если считать, что изменение суставных углов у спортсмена описывается функцией линейного характера (3.2.1), то закон изменения позы тела спортсмена в промежутке времени от t1 до t2 можно определить следующим образом.
Пользуясь изображениями поз тела на рис. 3.2.2а и 3.2.2б, в соответствии с правилами отсчета измерим суставные углы и запишем матрицы начальной и конечной поз тела (отсутствие указания матриц для движений типа 1: φ 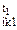 и φ
и φ 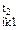 свидетельствует об их нулевом значении (в соответствии с правилом умалчивания)):
свидетельствует об их нулевом значении (в соответствии с правилом умалчивания)):
| 33 -102 -10 0 | t1 | 115 -104 -45 0 | t2 | |
| 33 -102 -10 0 | 115 -104 -45 0 | |||
φ  = =
| 115 0 0 0 | φ 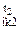 = =
| 135 0 0 0 | (3.2.5) |
| 98 0 0 0 | 115 0 0 0 | |||
| 0 40 0 0 | 2, | -55 -15 0 0 | 2. |
Определим изменение величин суставных углов:
| 82 -2 -35 0 | t1-2 | |
| 82 -2 -35 0 | ||
φ 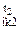 – φ – φ  = =
| 20 0 0 0 | (3.2.6.) |
| 17 0 0 0 | ||
| -55 -55 0 0 | ||
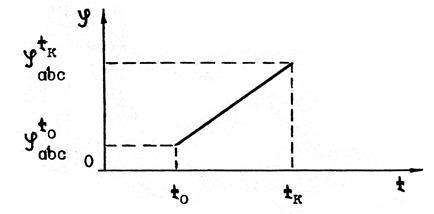
Рис. 3.2.1
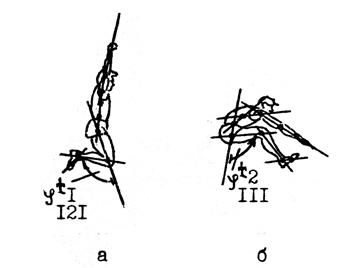
Рис. 3.2.2
Далее определим угловые скорости звеньев тела в процессе выполнения суставных движений, а также в соответствии с выражением (3.2.1) запишем закон изменения позы спортсмена при выполнении упражнения в промежутке времени от t1 до t2 (см. формулы 3.2.7 и 3.2.8).
| 410 -10 -175 0 | t1-2 | |
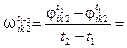
| 410 -10 -175 0 100 0 0 0 85 0 0 0 -275 -275 0 0 | (3.2.7) 2, |
| 410 -10 -175 0 | t1-2 | |
| 410 -10 -175 0 | ||
φ 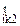 = φ = φ  + +
| 100 0 0 0 | × t (3.2.8) |
| 85 0 0 0 | ||
| -275 -275 0 0 | 2. |
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 462; Нарушение авторских прав?; Мы поможем в написании вашей работы!