
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная сложной функции. Табличные производные
|
|
|
|
Табличные производные
С помощью определения можно вычислять производные функций. Пример:
y= f(x)=x2 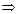 f(x+
f(x+  x)=(x+
x)=(x+  x)2=x2+2x
x)2=x2+2x  x+(
x+(  x)2
x)2 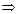
 y=
y=
f(x+  x) - f(x)=2x
x) - f(x)=2x  x+(
x+(  x)2.
x)2.
Отсюда 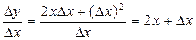 и
и 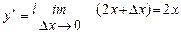
Совершенно аналогично можно получить и производные любых других функций. На этой основе разработана и постоянно используется стандартная таблица производных:
| у=С | 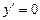 С – постоянное (число) С – постоянное (число)
| |
| у=xa | 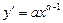 a a 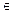 R R
| |
| у=sin x | 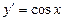
| |
| у=cos x | 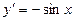
| |
| у=tg x | 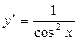
| |
| у=ctg x | 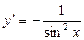
| |
| у=ax | 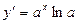
| |
| у=ex | 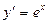
| |
| у=logax | 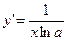
| |
| у=ln x | 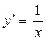
| |
| у=arcsin x | 
| |
| у= arccos x | 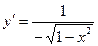
| |
| у=arctg x | 
| |
| у=arcctg x | 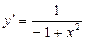
|
Теоремы дифференцирования
Так же, как и при вычислении пределов, математика разработала ряд теорем, ускоряющих вычислительную работу. Приведем их без доказательств:
· Сумма: у=u(x) 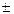 v(x)
v(x) 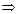
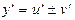 .
.
· Произведение: y=u 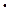 v
v 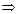
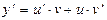 .
.
· Частное: y= 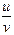

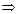
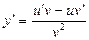
· Постоянный множитель: y=Cu 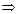
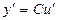

Как было показано в лекции 2 Функция, сложную функцию следует заменить эквивалентной системой. После этого полученную систему дифференцируем по каждому уравнению системы. Окончательный результат получается как произведение промежуточных:
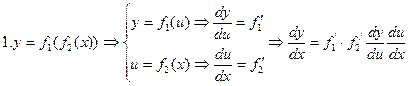
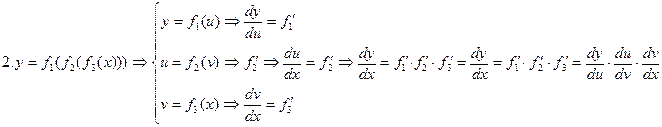
Совершенно аналогично представляются и рассчитываются и более громоздкие функции.
Производная неявной функции
Неявная функция включает в себя составляющие, которые содержат операции над у=f(x). Например, у2 или 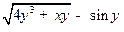 и т.п. Рассмотрим выражение F=
и т.п. Рассмотрим выражение F= 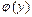 , где у=f(x). Подходя к нему как к сложной функции, запишем систему:
, где у=f(x). Подходя к нему как к сложной функции, запишем систему:

Это и есть правило дифференцирования неявной функции.
Пример: х2+у2= 100 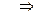
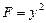
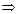
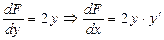
Следовательно, производная от данной неявной функции имеет вид:
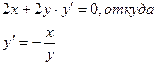
Производные высших порядков
Производная 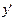 определяет, очевидно, некоторую новую функцию, которую, конечно, можно продифференцировать еще раз. По отношению к исходной функции у=f(x) это будет уже вторая производная
определяет, очевидно, некоторую новую функцию, которую, конечно, можно продифференцировать еще раз. По отношению к исходной функции у=f(x) это будет уже вторая производная 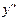 или
или 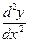 . Ясно, что этот процесс можно продолжать и получать все более высокие производные
. Ясно, что этот процесс можно продолжать и получать все более высокие производные 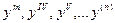 По-другому:
По-другому: 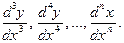
Пример: для у=sin x 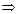
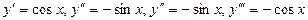 и т.д.
и т.д.
Только вторая производная имеет общефизический смысл - она характеризует «скорость изменения скорости» функции в точке, т.е. - ускорение.
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!