Уравнения для потенциала скоростей

Дифференциальная форма

Дифференциальная форма общего уравнения непрерывности такова:

где

• ∇• — дивергенция,
• t — время,
• j — плотность потока (см. ниже),
• σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно.

Это общее уравнение может быть использовано для вывода любого уравнения непрерывности, начиная с простого уравнения неразрывности и до уравнения Навье-Стокса.

Если q — сохраняющаяся величина, которая не может быть создана или уничтожена (например, энергия), тогда σ = 0, и уравнение непрерывности принимает вид:

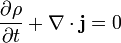
3 волновое уравнение для потенциала скоростей

1. Несжимаемая жидкость. Уравнение неразрывности для несжимаемой жидкости

Так как движение потенциально, то

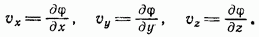
Подставляя в уравнение неразрывности, получаем уравнение для потенциала скоростей несжимаемой жидкости

Уравнение для есть уравнение Лапласа.

2. Сжимаемая жидкость. Рассматриваем безвихревое движение идеальной баротропной жидкости. Считаем, что массовые силы отсутствуют. В силу этих предположений можем написать

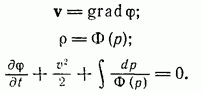(9.1)

Интеграл Лагранжа (9.3) заменяет уравнение Эйлера. К уравнениям (9.1), (9.2), (9.3) следует присоединить уравнение неразрывности

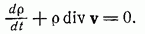
Наша задача — получить уравнение для потенциала скоростей .

Из (9.1) следует, что

Из (9.2), вводя скорость звука , получаем

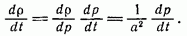
Уравнение неразрывности (9.4) согласно (9.5) и (9.6) можно переписать в виде

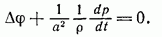
Из интеграла Лагранжа (9.3) следует

Подставим (9.8) в (9.7). С учетом равенства 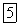будем иметь

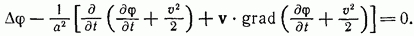
Здесь

Из (9.3) следует, что р есть функция суммы . Следовательно, есть функция производных от Таким образом, уравнение (9.9) есть уравнение для потенциала скоростей .

Введем в (9.9) выражение (9.10) для . Окончательно будем иметь

Частные производные второго порядка в уравнение (9.11) входят линейно, коэффициенты при них зависят от производных первого порядка. Уравнения, линейные относительно старших производных, называются квазилинейными. Уравнение служит для нахождения . После того как найдено, из (9.3) найдем р, а затем .

Предположим, что движение установившееся. В этом случае и уравнение (9.11) для потенциала принимает вид

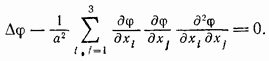
Введем обозначение

и перепишем уравнение (9.12) в виде

ИЛИ

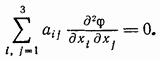
Обозначим определитель, составленный из коэффициентов через . В зависимости от знака D различают три типа уравнений (9.13): эллиптические уравнения, если ; гиперболические уравнения, если параболические, если D = 0. Непосредственно можно убедиться, что в нашем случае определитель D оказывается равным

Таким образом, уравнения являются эллиптическими, если , т. е. — скорость потока меньше скорости звука; уравнения гиперболические, если — скорость потока больше скорости звука.

Частный случай. Рассмотрим задачу о распространении малых возмущений в сжимаемой жидкости.

Пусть эти возмущения возникают в находящемся в равновесии покоящемся газе. Обозначим через , где параметры газа при . Гидродинамические величины можно в этом случае записать в виде

где — малые возмущения скорости, давления и плотности. Так как рассматривается потенциальное движение, то , где — потенциал возмущенного движения . Отбрасывая в уравнении (9.11) члены, содержащие малые величины в степени выше первой, получаем

Уравнение (9.16) — классическое волновое уравнение. Величина — скорость распространения звука в покоящемся газе. Найдя из решения (9.16), определим скорость . Определим давление, используя интеграл Лагранжа:

Так как жидкость баротропна, то , и можно найти р:

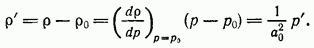
Давление и плотность также удовлетворяют волновому уравнению. В этом нетрудно убедиться, дифференцируя (9.16) по t и используя формулы (9.17) и (9.18). Заметим, что волновое уравнение для и можно получить непосредственно из системы уравнений идеальной сжимаемой жидкости. Подставив в систему соотношения (9.15) и исключив из уравнений, например, v и р, получим волновое уравнение для р.

Волновое уравнение (9.16) описывает распространение возмущений со скоростью . Проще всего в этом убедиться, рассматривая частные решения уравнения, зависящие только от . В этом случае (9.16) принимает вид

Общее решение уравнения (9.19)

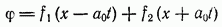
( — произвольные функции) описывает распространение двух волн, движущихся в противоположных направлениях со скоростью . Таким образом, скорость звука можно интерпретировать как скорость распространения малых возмущений в покоящемся газе. Законы распространения звука в движущейся и покоящейся средах изучает акустика.

4 плоские звуковые волны. Решение волнового уравнения.

Дата добавления: 2015-05-10