Формула Д'Аламбера

Решение волнового уравнения

Основная статья: Формула Кирхгофа

Существует аналитическое решение гиперболического уравнения в частных производных. В евклидовом пространстве произвольной размерности оно называется формулой Кирхгофа. Частные случаи: для колебания струны (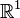) — формула Д’Аламбера, для колебания мембраны (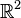) — формула Пуассона.

Решение одномерного волнового уравнения (здесь — фазовая скорость)

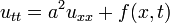(функция 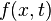соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид

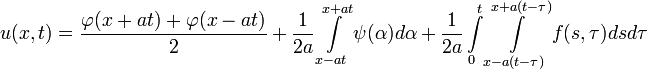
Интересно заметить, что решение однородной задачи

,

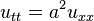имеющее следующий вид

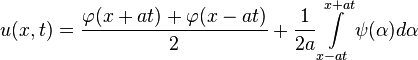
может быть представлено в виде

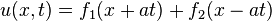
где

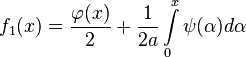
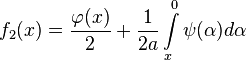
В таком случае говорят, что решение представлено в виде суммы бегущих волн, а функци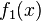и и 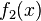- это профили волн, бегущих, соответственно, влево и вправо. В рассматриваемом случае профили волн со временем не изменяются.

В многомерном случае также решение задачи Коши может быть разложено в бегущие волны, однако уже не в сумму, а в интеграл, поскольку направлений становится бесконечно много. Это делается элементарно при помощи преобразования Фурье

5 плотность потока энергии звуковой волны. Акустическое сопротивление

Плотностью потока энергии — средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны

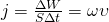
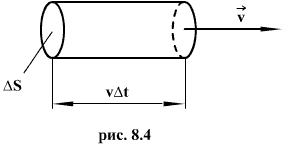
Через площадку S за время 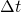будет перенесена энергия 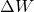заключенная в цилиндре с основанием S и высотой 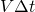. Если размеры цилиндра достаточно малы (за счет малости S и 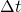) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то можно найти как произведение плотности энергии w на объем цилиндра, S и 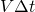и тогда получается, что энергия равна:

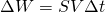
Подставим данную энергию в первоначальное уравнение и у нас получится:

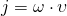
В Формуле мы использовали:

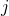— Интенсивность электромагнитной волны (плотностью потока энергии)

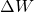— Энергия волны

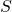— Площадь поверхности

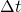— Время

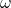— Плотность энергии

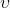— Скорость волны

Дата добавления: 2015-05-10