Энтропия

Адиабатический процесс.

АП - это процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим можно отнести все быстропротекающие процессы. Из 1-го начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что dA= -dU, т.е внешняя работа совершается за счет изменения внутренней энергии системы. Т.о, pdV= - m/M* C_vdT (1).

Продифференцировав ур-е состояния для идеального газа,pV=m/M*RT, получим

PdV + Vdp=m/M*RdT .(2)

Исключим из ур-я (1) и (2) температуру T: (pdV+Vdp)/(pdV)= - R/C_v= -(C_p-C_v)/ C_v.

Разделив переменные и учитывая, что C_p/C_v=g, найдем dp/p= - gdV/V.

Интегрируя это ур-е в пределах от p1 до p2 и соответственно от V1 до V2, а затем, потенцируя, придем к выражению p2/p1=(V1/V2)^g, или p1(V1)^g = p2(V2)^g.Так как состояния 1 и 2 выбраны произвольно, то можно записать

pV^g=const(ур-е адиабатического процесса или ур-е Пуассона).Здесь g - показатель адиабаты (или коэффициент Пуассона), g=(i+2)/i.

Вычислим работу, совершаемую газом в адиабатическом процессе: dA= -m/M* C_vdT.

Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа

A= - m/M*C_vòdT=m/M* C_v(T1-T2).

Изохорный, изобарный, изотермический и адиабатический процессы имеют одну особенность – они происходят при постоянной теплоемкости.

Эквиваленты теплоты и работы.

Обмен энергией между термодинамической системой и внешними телами может осуществляться 2мя качественно различными способами: путем совершения работы и путем теплообмена. В отсутствии внешних полей работа совершается при изменении объема или формы системы. Работа A', совершаемая внешнми телами над системой численно равна и противоположна по знаку работе, совершаемой самой системой.

Помимо внутренней энергии, которая является только функциональной составляющей термодинамической системы, в термодинамике используется еще ряд других функций, описывающих состояние термодинамической системы. Особое место среди них занимает энтропия. Пусть Q - теплота, полученная термодинамической системой в изотермическом процессе, а T - температура, при которой произошла эта передача теплоты. Величина Q/ T называется приведенной теплотой. Приведенное количество теплоты, сообщаемое термодинамической системе на бесконечно малом участке процесса будет равно dQ / T. В термодинамике доказывается, что в любом обратимом процессе сумма приведенных количеств теплоты, передаваемая системе на бесконечно малых участках процесса равна нулю. Математически это означает, что dQ/T - есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от того, каким путем перешла система в такое состояние. Функция, полученный дифференциал которой равен dS= dQ/ T - называется энтропией. Энтропия определяется только состоянием термодинамической системы и не зависит от способа перехода системы в это состояние. S - энтропия. Для обратимых процессов delta S = 0. Для необратимых delta S > 0 - неравенство Клаудио. Неравенство Клаудио справедливо только для замкнутой системы. Только в замкнутой системе процессы идут так, что энтропия возрастает. Если система незамкнута и может обмениваться теплотой с окружающей средой, ее энтропия может вести себя любым образом; dQ = T dS; При равновестном переходе системы из одного состояния в другое dQ = dU + dA; delta S = (интеграл 1 - 2) dQ / T = (интеграл) (dU + dA) / T. Физический смысл имеет не сама энтропия, а разность энтропий при переходе системы из одного состояния в другое.

Связь энтропии с вероятностью состояния системы.

Более глубокий смысл энтропии скрывается в статической физике. Энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность состояния системы - это число способов, которыми может быть реализовано данное состояние макроскопической системы. Иными словами W - это число микросостояний, которые реализовывают данные макросостояния.

Больцман методами статистической физики показал, что энтропия S системы и термодинамическая вероятность связаны соотношением: S= k ln (W); где k - постоянная Больцмана. Термодинамическая вероятность W не имеет с математической вероятностью ничего общего. Из этого соотношения видно, что энтропия может рассматриваться как мера вероятности состояния термодинамической системы, энтропия является мерой неупорядоченной системы. Чем больше число микросостояний, реализующих данное макросостояние, тем больше ее энтропия.

Второй закон термодинамики.

Количество теплоты, полученное от нагревателя, не может быть целиком преобразовано в механическую работу циклически действующей тепловой машиной. Это и есть 2ой закон: в циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от источника энергии - нагревателя. (by Кельвин Copyright 1851). Второй закон связан с необратимостью процессов в природе. Возможна другая формулировка: невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от холодного тела к горячему. Второй закон имеет вероятный характер. В отличие от закона сохранения энергии, второй закон применим лишь к системам, состоящим из очень большого числа частиц. Для таких систем необратимость процессов объясняется тем, что обратный переход должен был бы привести систему в состояние ничтожно малой вероятностью, практически не отличимой от невозможности.

Самопроизвольные процессы в изолированной системе всегда проходят в направлении перехода от маловероятного состояния в более вероятное.

Цикл Карно.

Для создания тепловой машины недостаточно просто иметь нагретое тело (нагреватель), требуется еще 2-е тело – холодильник. Т.о, рабочее тело передает теплоту от нагревателя к холодильнику и попутно совершает полезную работу.

p

В качестве рабочего тела Сади Карно выбрал идеальный газ. Он рассмотрел следующий процесс:

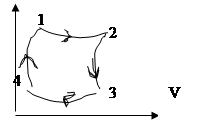
Кривые 1-2, 3-4 – изотермы, кривые 2-3,4-1 – адиабаты.

На участке 1-2 газ получает теплоту Q1 от нагревателя и, расширяясь, совершает работу (т.е расходует полученное Q1 на совершение работы). Q1=∆U+A1, ∆U=0, т.к. T=const. Q1=A1.

На участке 2-3: газ совершает работу А2, которая равна убыли внутренней энергии; температура понижается. А2= - ∆U2 (температура понижается от Т1 до Т2).

На участке 3-4: V уменьшается, Т2=const. Внешние силы совершают работу по сжатию газа A3: Q2= -A3, Q2=A′. От системы отводится количество теплоты Q2: |Q2|=A3.

На участке 4-1: V уменьшается, T увеличивается. A’4=∆U, Q=∆U+A, 0= ∆U4 + A4 =∆U4-A’4, A’4=∆U (внешние силы совершили работу, которая пошла на увеличение внутренней энергии.

Для изотерм A=A1+A3=Q4-|Q2|.

Площадь под изотермой 3-4 меньше, чем под изотермой 1-2 Þ |A’3|<|A1|, Q1>Q2 Þ газ получает от нагревателя больше теплоты, чем отдает холодильнику.

За полный цикл: ∆U=0, А=А1 – А’3 - ∆U2(=A2) + A’4, ∆U2=3/2*m / M*R(T2-T1).

A=Q1-|Q2| - 3/2*m/M*R(T2-T1) + (-3/2*m/M*R(T1-T2))=Q1-|Q2|.

Коэффициентом полезного действия тепловой машины называется отношение полезной работы, совершаемой за цикл, к количеству теплоты, полученной системой. Выражается в процентах. h=(Q1-|Q2|)/Q1 * 100% (1), или h=A/Q1 *100% (2). Эти формулы можно использовать для любой тепловой машины.

Теорема Карно: Q1/T1=|Q2|/T2 (для машины Карно). h=(T1-T2)/T1 *100%.

КПД, определяемый формулами (1) и (2) – наибольший возможный. В реальных тепловых машинах КПД меньше.

Дата добавления: 2015-05-10