Детерминированные сигналы

Классификация детерминированных сигналовосуществляется на основании существенных признаков соответствующих математических моделей сигналов. Обычно выделяют два класса детерминированных сигналов: периодические и непериодические.

К периодическим относят гармонические и полигармонические сигналы.

Гармонические сигналы (Рис. 2.3.1), описываются следующими формулами:

s (t) = A sin(2π f₀t +φ) = A sin(ω₀ t + φ) или s (t) = A× cos(ω ₀ t +f),

где А, f₀, ω₀, φ, f - постоянные величины: А - амплитуда сигнала, f₀ - циклическая частота в герцах, ω₀ - угловая частота в радианах, j и f - начальные фазовые углы в радианах. Период одного колебания 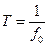. При j = f - p/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и фазовым значением одной частоты.

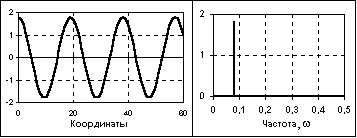
Рис. 2.3.1. Гармонический сигнал и его АЧХ.

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов (Рис. 2.3.2) и описываются выражениями:

,

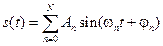или: s (t) = y (t ± kT_p), k = 1,2,3,..., где Т_p - период одного полного колебания сигнала. Число циклов колебаний за единицу независимой переменной t называют фундаментальной частотой 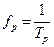. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей и произвольного (в пределе - бесконечного) числа гармонических составляющих с частотами, кратными фундаментальной частоте f_p, и с произвольными значениями амплитуд A_n и фаз j _n. Другими словами, частотный спектр полигармонических сигналов дискретен, поэтому получило широкое распространение математическое представление сигналов - в виде спектров (рядов Фурье).

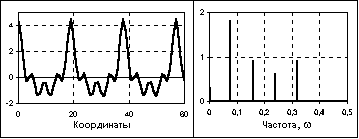
Рис. 2.3.2. Полигармонический сигнал и его АЧХ.

К непериодическим сигналам относят почти периодические и апериодические сигналы.

Почти периодические сигналы близки по своей форме к полигармоническим (Рис. 2.3.3). Они также представляют собой сумму двух и более гармонических сигналов, но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Например,

.

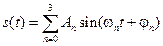Естественно, частотный спектр почти периодических сигналов также дискретен.

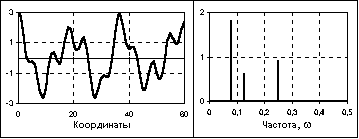
Рис. 2.3.3. Почти периодический сигнал и его АЧХ.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На Рис. 2.3.4 показан пример такого сигнала, заданного формулой на интервале (0, ¥): s (t) = exp(-0.15 t) - exp(-0.17 t).

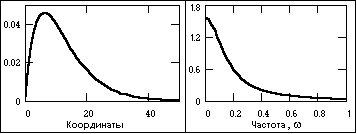
Рис. 2.3.4. Апериодический сигнал и модуль его спектра.

Частотный спектр апериодических сигналов непрерывен и для их представления в частотной области используется интегральное преобразование Фурье.

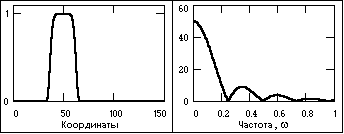
Рис. 2.3.5. Импульсный сигнал и модуль его спектра.

К апериодическим сигналам относятся также и импульсные сигналы. Импульсы представляют собой сигналы достаточно простой формы (Рис. 2.3.5), существующие в пределах конечных временных интервалов.

В классе импульсных сигналов выделяют подкласс радиоимпульсов. Пример радиоимпульса приведен на Рис. 2.3.6. Уравнение радиоимпульса имеет вид:

s (t) = u (t)cos(2π f₀t +f ₀),

где cos(2π f₀t +f ₀) - гармоническое колебание заполнения радиоимпульса, u (t) – огибающая радиоимпульса или видеоимпульс.

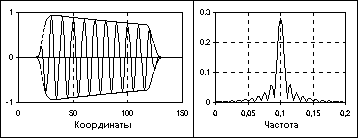
Рис. 2.3.6. Радиоимпульс и модуль его спектра.

Дата добавления: 2015-05-10