Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

• отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
• уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10^-3. Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10^-5. Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

• f(x) – функция левой части уравнения f(x) = 0;
• x – переменная, относительно которой требуется решить уравнение;
• a, b (необязательные) – действительные числа, такие что a < b, причем на интервале [ a, b ] находится только один корень.

Если функция root не может найти корни уравнения, то рекомендуется уточнить начальное приближение по графику, изменить границы интервала [ a, b ] нахождения корня или увеличить значение системной переменной TOL.

Для решения уравнений или систем нескольких уравнений и неравенств используются функции Find или Minerr. Они входят в состав вычислительного блока, который включает в себя ключевое слово Given, набор уравнений и неравенств и завершается одной из указанных вычисляющих функций в составе какого-нибудь выражения.

Функция

Find(x1, x2, …)

возвращает значения неизвестных x1, x2, …, обращающих уравнения в верные тождества, т. е. возвращает точное решение системы уравнений или одного уравнения в частном случае. Для системы из n уравнений с n неизвестными решение возвращается в виде вектора, состоящего из n элементов.

Если в результате поиска не может быть получено решение с заданной точностью, то функция Find выдает сообщение об ошибке. В этом случае можно использовать функцию

Minerr(x1, x2, …),

возвращающую приближенное решение системы уравнений или одного уравнения (число уравнений должно быть равно числу неизвестных). При использовании minerr необходимо производить дополнительную проверку достоверности результатов решения системы.

Порядок применения блоков Given…Find, Given…Minerr для численного решения уравнений и систем уравнений:

1. Всем неизвестным, входящим в систему, задается начальное приближение.
2. При необходимости присваиваются требуемые значения системным переменным TOL и CTOL (Constraint Tolerance – Допуск ограничения).
3. Печатается ключевое слово Given, которое указывает Mathcad, что далее следует система уравнений.
4. Задаются уравнения и ограничения на поиск решения в виде неравенств (если они имеются) в любом порядке, каждое в отдельном формульном блоке, причем для записи используются операторы отношения палитры Boolean (Логические). Допускается использование двусторонних неравенств вида a ≤ x ≤ b.
5. Применяется функция Find или Minerr в составе какого-нибудь выражения. В качестве аргументов через запятую перечисляются имена входящих в систему переменных в том порядке, в котором должны быть расположены в ответе соответствующие им корни.
6. В случае использования функции Minerr выполняется проверка.

Внутри блока решения недопустимы следующие операции и выражения:

• ранжированные переменные;
• выражения, содержащие знак ≠;
• локальное (:=) или глобальное (Ξ - тождественно равно) определение переменных и функций, за исключением выражения, в состав которого входит функция Find или Minerr;
• другой блок решения. Каждый блок должен содержать только одно слово Given и одну решающую функцию.

В случае появления ошибки , означающей, что решение не было найдено, рекомендуется изменить начальное приближение или значения системных переменных TOL и CTOL.

Решение полиномиальных уравнений. Функция polyroots

Для решения полиномиальных уравнений вида

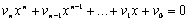
или нахождения всех корней полинома степени n, используют функцию

polyroots(v),

возвращающую вектор-столбец длины n, состоящий из корней полинома, как действительных, так и комплексных. Аргументом функции polyroots является вектор v длины n + 1 < 100, содержащий коэффициенты полинома.

Решить полиномиальное уравнение можно следующим образом:

1. задать полином;
2. выделить переменную синим управляющим курсором;
3. создать вектор коэффициентов полинома, выполнив последовательность команд главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома);
4. вырезать вектор коэффициентов полинома в буфер обмена;
5. задать переменную v и присвоить ей значение вектора коэффициентов полинома, вставив его непосредственно из буфера обмена;
6. применить функцию polyroots(v) в каком-нибудь выражении, например, X:=polyroots(v);
7. получить вектор корней полинома: X =.

Решение систем линейных уравнений

Рассмотрим систему линейных алгебраических уравнений:

В матричном виде ее можно записать Ax = b,

где 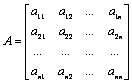– матрица коэффициентов при неизвестных системы (матрица левой части системы);

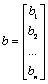– столбец свободных членов.

Как известно, система линейных алгебраических уравнений имеет решение, если ее определитель отличен от 0: det(A)=| A |≠0.

Умножим обе части матричного уравнения Ax = b на обратную матрицу коэффициентов при неизвестных системы A ^-1 слева: A ^-1 Ax = A ^-1 b. Учитывая, что A ^-1 A, вектор-столбец решений системы можно искать в виде

x = A ^-1 b.

Этот прием используется в Mathcad так:

1. задается матрица коэффициентов при неизвестных системы A;
2. задается столбец свободных членов b;
3. вводится формула для нахождения решения системы X:=A ^-1 b;
4. выводится вектор решений системы X =.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A ^-1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref (M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

1. Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
2. Сохранить в личной папке на диске z:\ новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3. Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

1. В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
2. Выполнить задание 1.

Задание 1. Решить уравнение .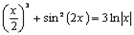

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f (x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

x:=-5,-4.9..5

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f (x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f (x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

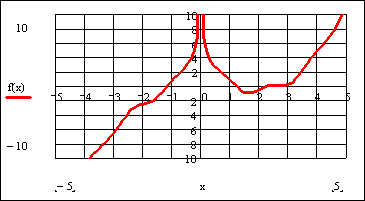
Из графика функции f(x) видно, что уравнение 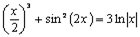имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

x:=-1 TOL:=0.0001

Уточним заданное приближение к значению корня с помощью функции root:

x1:=root(f(x),x)

x1=-1.1395

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

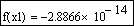
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

1. Выполнить задание 2.

Задание 2. Решить уравнение .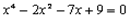

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

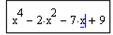
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v:= и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

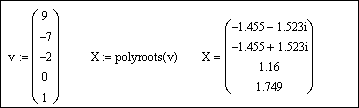
1. Выполнить задание 3.

Задание 3. Решить систему линейных уравнений 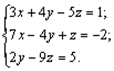Сделать проверку.

Дата добавления: 2015-05-10