Теоретические сведения. Возможные поражения личного состава а районе разлива

Возможные поражения личного состава а районе разлива

Определение возможных потерь людей в очаге химического поражения

Потери рабочих, служащих, а. также личного состава формирований ГО будут зависеть от количества людей, оказавшихся в очаге поражения, степени их защищенности и своевременного использования средств индивидуальной защиты (противогазов). Возможные потери людей в очаге поражения определяются по таблице 10.

Таблица 10

и зонных заражений, %

Условия нахождения людей	Обеспеченность людей противогазами (%)
На открытой местности
В простейших укрытиях, зданиях

Примечание: Ориентировочная структура потерь

- легкой степени – 25% (не нуждаются в госпитализации);

- средней и тяжелой степени – 40 % (нуждаются в госпитализации);

- со смертельным исходом - 35 %.

.

Пример: На химическом заводе в результате аварии разрушена емкость с хлором. Вся территория завода находится в зоне химического заражения. Рабочие и служащие (500 человек) находились на рабочих местах, в зданиях завода и обеспечены противогазами на 100%. Определить возможные потери.

Решение:

- по таблице 10 определяем, что потери рабочих и служащих будут составлять 4 процента т. е. 20 человек.

Согласно примечанию к таблице 10 количество пораженных легкой степени соответствует 25% (т.е. 5 человек из 20-ти). Их к количеству пораженных можно не причислять. Итак, потери составят не более 15 человек.

Пусть уравнение имеет вид 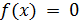. Функция определена в некотором конечном или бесконечном интервале . Всякое значение , обращающее функцию в нуль называется корнем уравнения. При отыскании приближенных значений корней уравнения приходится решать две задачи:

- Отделение корней. Отыскиваются ограниченные области, в каждой из которых заключен один и только один корень уравнения.

- Вычисление корней с заданной точностью.

При отделении корней уравнения полезны следующие теоремы:

Теорема 1. Если непрерывная функция 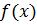принимает значение разных знаков на концах промежутка так, что 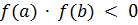, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения .

Для нашего случая . Выберем промежуток, на котором будем определять наименьший положительный корень с помощью построения графика заданной функции:

Рисунок 1. График исследуемой функции.

Выберем промежуток :

Рисунок 2. Промежуток, выбранный для определения корня.

Проверим выполнение теоремы 1 для выбранного промежутка:

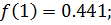
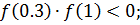
Теорема 1 выполняется.

Теорема 2. Корень будет единственным, если при выполнении условий, изложенных в предыдущей теореме, производная 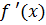существует и сохраняет постоянный знак внутри .

Для проверки монотонности функции на промежутке нужно найти корни производной , которые укажут интервалы, подозрительные на содержание искомого корня функции . На концах этих интервалов проверяется условие первой теоремы. Если оно выполняется, то интервал содержит корень.

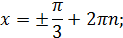
n – целое положительное число

Выбранный нами интервал находится в интервале [-π/3; π/3], где -π/3 и π/3 – точки, подозрительные на экстремум. Проверим выполнение условия первой теоремы:

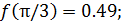
Первая теорема выполняется, следовательно, функция 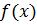монотонна на промежутке и содержит искомый корень.

Метод касательных (метод Ньютона)

Дана функция , непрерывная на и удовлетворяющая условию . Очередное приближение 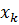корня в методе касательных вычисляется по формуле

,

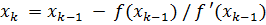где - предыдущее приближение корня, значения функции и ее первой производной в точке .

В качестве начального приближения 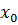принимается одна из границ отрезка, удовлетворяющая условию

Вычисления корня прекращаются при условии, что

где 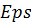– точность вычисления корня.

Проверим условие начального приближения на границах отрезка. Для этого вычислим вторую производную:

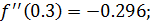
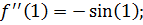
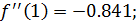
В качестве начального приближения возьмём точку

Вычислим несколько приближений для :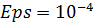

Первое приближение:

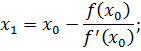
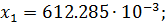
второе приближение:

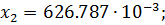
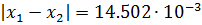
Третье приближение:

Для 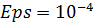решением является .

Дата добавления: 2015-05-10