Канонические уравнения прямой

Как составить уравнения прямой в пространстве?

УравнениЯ прямой в пространстве

Аналогично «плоской» прямой, существует несколько способов, которыми мы можем задать прямую в пространстве. Начнём с канонов – точки и направляющего вектора прямой:

Если известна некоторая точка пространства 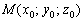, принадлежащая прямой, и направляющий вектор 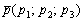данной прямой, то канонические уравнения этой прямой выражаются формулами:

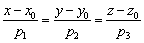
Приведённая запись предполагает, что координаты направляющего вектора 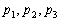не равны нулю. Что делать, если одна или две координаты нулевые, мы рассмотрим чуть позже.

Как и в статье Уравнение плоскости, для простоты будем считать, что во всех задачах урока действия проводятся в ортонормированном базисе пространства.

Пример 1

Составить канонические уравнения прямой по точке 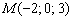и направляющему вектору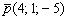

Решение: Канонические уравнения прямой составим по формуле:

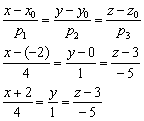
Ответ: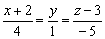

И ежу понятно… хотя, нет, ежу не понятно вообще ничего.

Что следует отметить в этом очень простом примере? Во-первых, полученные уравнения НЕ НАДО сокращать на единицу: . Сократить, точнее, можно, но это непривычно режет глаз и создаёт неудобства в ходе решения задач.

А во-вторых, в аналитической геометрии неизбежны две вещи – это проверка и зачёт:

На всякий случай смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны координаты направляющего вектора 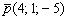. Нет, не подумайте, у нас не урок в детском садике «Тормозок». Данный совет очень важен, поскольку позволяет полностью исключить ошибку по невнимательности. Никто не застрахован, а вдруг неправильно переписали? Наградят премией Дарвина по геометрии.

Далее подставляем координаты точки 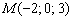в найденные уравнения:

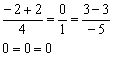
Получены верные равенства, значит, координаты точки 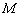удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.

Проверка очень легко (и быстро!) выполняется устно.

В ряде задач требуется найти какую-нибудь другую точку 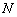, принадлежащую данной прямой. Как это сделать?

Берём полученные уравнения 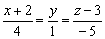и мысленно «отщипываем», например, левый кусочек: 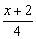. Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: 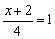. Так как 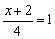, то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:

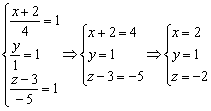
Проверим, удовлетворяет ли найденная точка 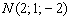уравнениям :

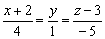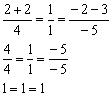
Получены верные равенства, значит, точка 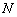действительно лежит на данной прямой.

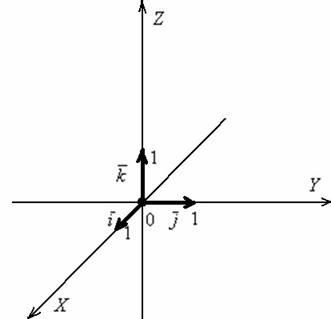
Выполним чертёж в прямоугольной системе координат. Заодно вспомним, как правильно откладывать точки в пространстве:

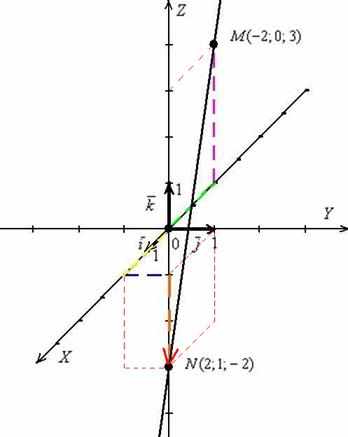
Строим точку :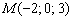
– от начала координат в отрицательном направлении оси 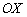откладываем отрезок первой координаты 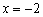(зелёный пунктир);
– вторая координата 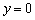нулевая, поэтому «не дёргаемся» с оси 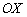ни влево, ни вправо;
– в соответствие с третьей координатой 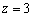отмеряем три единицы вверх (фиолетовый пунктир).

Строим точку 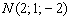: отмеряем две единицы «на себя» (желтый пунктир), одну единицу вправо (синий пунктир) и две единицы вниз (коричневый пунктир). Коричневый пунктир и сама точка 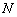наложились на координатную ось, обратите внимание, что они находятся в нижнем полупространстве и ПЕРЕД осью .

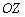Сама прямая 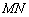проходит над осью 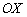и, если меня не подводит глазомер, над осью 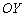. Не подводит, убедился аналитически. Если бы прямая 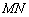проходила ЗА осью 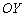, то следовало бы стереть ластиком частичку линии 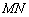сверху и снизу точки скрещивания.

У прямой бесконечно много направляющих векторов, например:
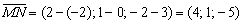(красная стрелка)

Получился в точности исходный вектор 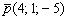, но это чистая случайность, такую уж я выбрал точку 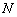. Все направляющие векторы прямой коллинеарны, и их соответствующие координаты пропорциональны (более подробно – см. Линейная (не) зависимость векторов. Базис векторов). Так, векторы 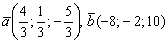тоже будут направляющими векторами данной прямой.

Дополнительную информацию о построении трёхмерных чертежей на клетчатой бумаге можно найти в начале методички Графики и свойства функций. В тетради разноцветные пунктирные дорожки к точкам (см. чертёж) обычно тонко прочерчивают простым карандашом тем же пунктиром.

Разберёмся с частными случаями, когда одна или две координаты направляющего вектора нулевые. Попутно продолжаем тренировку пространственного зрения, которая началась в начале урока Уравнение плоскости. И вновь я расскажу вам сказку о голом короле – нарисую пустую систему координат и буду убеждать вас, что там есть пространственные прямые =)

Проще перечислить все шесть случаев:

1) Для точки 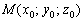и направляющего вектора 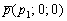канонические уравнения прямой распадаются на три отдельных уравнения: .

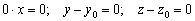Или короче: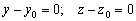

Пример 2: составим уравнения прямой по точке 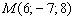и направляющему вектору :

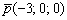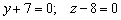
Что это за прямая? Направляющий вектор прямой 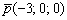коллинеарен орту 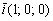, значит, данная прямая будет параллельна оси 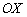. Канонические уравнения следует понимать так:
а) 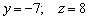– «игрек» и «зет» постоянны, равны конкретным числам;
б) переменная «икс» может принимать любые значения: 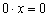(на практике данное уравнение, как правило, не записывают).

В частности, уравнения 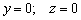задают саму ось 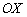. Действительно, «икс» принимает любое значение, а «игрек» и «зет» всегда равны нулю.

Рассматриваемые уравнения можно интерпретировать и другим образом: посмотрим, например, на аналитическую запись оси абсцисс: 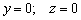. Ведь это уравнения двух плоскостей! Уравнение 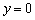задаёт координатную плоскость 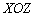, а уравнение 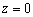– координатную плоскость 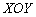. Правильно думаете – данные координатные плоскости пересекаются по оси 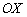. Способ, когда прямая в пространстве задаётся пересечением двух плоскостей, мы рассмотрим в самом конце урока.

Два похожих случая:

2) Канонические уравнения прямой, проходящей через точку 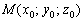параллельно вектору 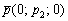, выражаются формулами .

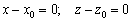Такие прямые будут параллельны координатной оси 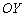. В частности, уравнения 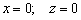задают координатную саму ось ординат.

3) Канонические уравнения прямой, проходящей через точку 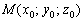параллельно вектору 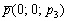, выражаются формулами .

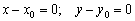Данные прямые параллельны координатной оси 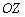, а уравнения 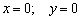задают саму ось аппликат.

Загоним в стойло вторую тройку:

4) Для точки 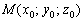и направляющего вектора 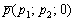канонические уравнения прямой распадаются на пропорцию 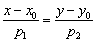и уравнение плоскости .

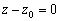Пример 3: составим уравнения прямой по точке 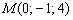и направляющему вектору :

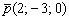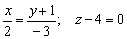
Разберём суть полученной записи. Уравнение 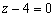задаёт плоскость в пространстве, причём данная плоскость будет параллельна «родной» координатной плоскости 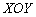. Из пропорции 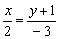легко выразить уравнение «плоской» прямой, единственное, эта прямая будет находиться не на плоскости 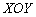, а на высоте .

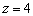Если высота нулевая: 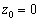, то уравнения принимают вид 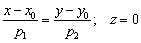, и вот это уже в точности наша «плоская» прямая, лежащая в плоскости .

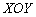Таким образом, рассмотренный случай задаёт прямую, параллельную координатной плоскости 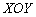. Действительно, задумайтесь, ведь направляющий вектор 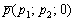параллелен данной плоскости, ведь «зетовая» координата равна нулю.

5) Прямая, заданная точкой 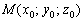и направляющим вектором 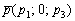, параллельна координатной плоскости 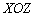, и её канонические уравнения выражаются формулами: .

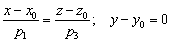В частности, уравнения 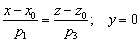определяют прямую, лежащую в плоскости .

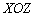6) Прямая, заданная точкой 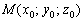и направляющим вектором 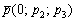, параллельна координатной плоскости 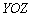, и её канонические уравнения выражаются формулами: .

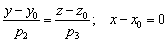В частности, уравнения 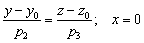определяют прямую, лежащую в плоскости .

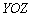Настала пора хорошо закусить:

Пример 4

Записать канонические уравнения прямой, если известна точка и направляющий вектор данной прямой.

а)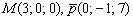
б)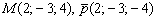
в) Записать уравнения прямой, проходящей через точку 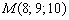параллельно оси .

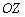Это примеры для самостоятельного решения, ответы в конце урока.

Постарайтесь не пренебрегать примерами данного урока! Задачи вроде бы элементарны, но если на них забить, то в дальнейшем появятся серьёзные затруднения. Причём, в простых вещах.

Дата добавления: 2015-05-10