Параметрические уравнения прямой в пространстве

Обязательно прочитайте данный параграф! Параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но рабочий муравей многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.

Если известна точка 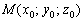, принадлежащая прямой, и направляющий вектор 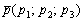данной прямой, то параметрические уравнения этой прямой задаются системой:

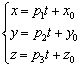
О самом понятии параметрических уравнений я рассказывал на уроках Уравнение прямой на плоскости и Производная параметрически заданной функции.

Всё проще пареной репы, поэтому придётся приперчить задачу:

Пример 7

Составить параметрические уравнения следующих прямых:

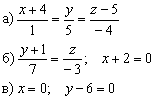
Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

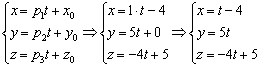
Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку 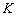, координаты которой, скажем, соответствуют значению параметра :

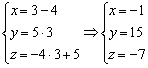
Таким образом: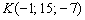

б) Рассмотрим канонические уравнения 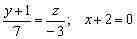. Выбор точки здесь несложен, но коварен: (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор 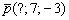, а на оставшееся место поставим ноль: .

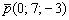Составим параметрические уравнения прямой:

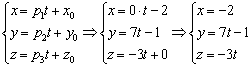
в) Перепишем уравнения 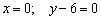в виде 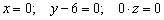, то есть «зет» может быть любым. А если любым, то пусть, например, 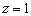. Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях 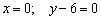находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: . На оставшееся место ставим единицу: 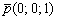. Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой:

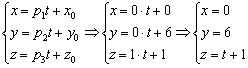
Для тренировки:

Пример 8

Составить параметрические уравнения следующих прямых:

Решения и ответы в конце урока. Полученные вами ответы могут несколько отличаться от моих ответов, дело в том, что параметрические уравнения можно записать не единственным способом. Важно, чтобы ваши и мои направляющие векторы были коллинеарны, и ваша точка «подходила» к моим уравнениям (ну, или наоборот, моя точка к вашим уравнениям).

Как ещё можно задать прямую в пространстве? Хочется что-нибудь придумать с вектором нормали. Однако номер не пройдёт, у пространственной прямой нормальные векторы могут смотреть совершенно в разные стороны.

Ещё об одном способе уже упоминалось на уроке Уравнение плоскости и в начале этой статьи:

Дата добавления: 2015-05-10