Тема 1.2. Метрологические показатели средств измерения

Основные методы решения рациональных уравнений.

1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax² + bx + c = 0 решаются по выведенной нами формуле

Также используется теорема Виета: x₁ + x₂ = – b / a; x₁x₂ = c / a.

2) Группировка: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа — ноль. Затем приравниваем к нулю каждый из сомножителей.

3) Подстановка: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно что удобно обозначить. Например, уравнение

(x² + x – 5) / x + 3x / (x² + x – 5) + 4 = 0,

легко решается с помощью подстановки (x² + x – 5) / x = t, получаем t + (3 / t) + 4 = 0.

Или: 21 / (x² – 4x + 10) – x² + 4x = 6. Здесь можно сделать подстановку x² – 4 = t. Тогда 21 / (t + 10) - t = 6 и т.д.

В более сложных случаях подстановка видна лишь после нескольких преобразований. Например, дано уравнение

(x² + 2x)² – (x +1)² = 55.

Переписав его иначе, а именно (x² + 2x)² – (x² + 2x + 1) = 55, сразу увидим подстановку x² + 2x=t.

Имеем t² – t – 56 = 0, t₁ = – 7, t₂ = 8. Осталось решить x² + 2x = – 7 и x² + 2x = 8.

В ряде других случаев удобную подстановку желательно знать “заранее”. Например

1. Уравнение (x + a)⁴ + (x + b)⁴ = c сводится к биквадратному, если сделать подстановку

x = t – (a + b) / 2.

2. Симметрическое уравнение (возвратное) a₀xⁿ + a₁x^{n – 1} + … + a₁x + a₀ = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1 / x = t, если n —чётное; если n — нечётное, то уравнение имеет корень x = – 1.

3. Уравнение вида (x + a)(x + b)(x + c)(x + d) = l сводится к квадратному, если a + b = c + d и т.д.

4) Подбор: при решении уравнений высших степеней рациональные корни уравнения a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₁x + a₀ = 0 ищем в виде p / q, где p — делитель a₀, q — делитель a_n, p и q взаимно просты, pÎ Z, qÎ N.

5) “Искусство”, т.е. решать пример нестандартно, придумать “свой метод”, догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.

6) Уравнения с модулем: при решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что

f (x), если f (x) ³ 0,

| f (x) | =– f (x), если f (x) < 0.

Виды ошибок, их классификация по форме числового выражения, по закономерности появления, по вероятности реализации.

Систематические погрешности, их задание и оценка. Случайные погрешности, источники их появления. Законы распределения погрешностей. Характеристики нормального распределения. Выявление промахов.

Погрешности как характеристики средств измерений. Виды погрешностей и основные причины их возникновения. Определение приборной погрешности на основании класса точности прибора. Предел, цена деления, чувствительность электроизмерительного прибора. Типовая методика проверки электроизмерительных приборов. Общие сведения обработки результатов измерений.

Методические указания

При изучении темы обратить внимание на виды погреш­ностей, причины, их вызывающие. Уяснить, что любое из­мерение должно проходить по системе: планирование, про­ведение измерений, математическая обработка результа­тов измерений. При обработке обращать внимание на вы­явление промахов. Очень важно научиться рассчитывать результирующую погрешность, знать, как суммируются систематические и случайные погрешности, как определя­ется результирующая погрешность с заданным уровнем вероятности.

В зависимости от причин погрешности подразделяют на пять групп: погрешности метода измерения, инструментальные, настройки прибора и его взаимодействия с объектом измерения, динамические и субъективные погрешности.

Погрешности метода измерения являются результатом вы­бранной схемы измерения, не позволяющей устранить источники известных погрешностей.

Инструментальные погрешности зависят от несовершенства измерительных устройств, т. е. от погрешностей изготовления деталей измерительного прибора.

Погрешности на­стройки измерительных приборов определяются условиями экс­плуатации. Погрешности могут возникать при взаимодействии прибора с объектом измерения; например, такие погрешности, которые вызываются влиянием измерительного усилия на де­формацию измеряемой детали.

Динамические погрешности возни­кают при преобразовании измеряемой величины. Динамические погрешности появляются в результате инерционности изменения измеряемого параметра.

Субъективные погрешности появляются вследствие ограниченных физических возможностей оператора.

В зависимости от условий работы различают два вида погреш­ностей: основные и дополнительные.

Основные погрешности имеют место при нормальных режимах работы измерительного прибора, когда влияние внешних факторов минимально.

Дополнительные погрешности вызываются воздействием внешних факторов, нару­шающих нормальные условия работы прибора, например, измене­нием температуры или давления окружающей среды.

Если значение абсолютной погрешности 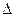отнести к истинному значению А0 измеряемого параметра, то получим относительную погрешность 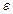, т. е.

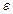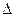= / А0.

Отношение абсолютной погрешности 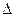к диапазону шкалы прибора N называют приведенной относительной погрешностью 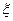, т. е.

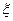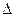= /N.

Вопросы для самопроверки

1. По каким признакам классифицируются ошибки?

2. Чем отличается относительная ошибка от приведен­ной?

3. Какие показатели применяются для характеристики случайной погрешности?

4. Каким образом можно выявить «промах» в ряде по­лученных результатов измерений?

5. В чем отличие равноточных измерений от неравно­точных?

6. Какова методика обработки результатов косвенных измерений?

7. Как рассчитать результирующую погрешность?

Раздел 2 Приборы и методы электрических измерений

Дата добавления: 2015-05-10