Уравнения Максвелла в интегральной форме

Система уравнений Максвелла

Система уравнений Максвелла предложена в 1864 г. Дж. К. Максвеллом как результат обобщения экспериментальных законов электромагнетизма и опубликована в виде 12 уравнений в 1873 г. Современная форма системы уравнений Максвелла (7 уравнений) была получена О. Хевисайдом и Г. Герцем [6].

Из высказываний современников Максвелла о его теории и системе уравнений стоит упомянуть высказанную Л. Больцманом цитату из «Фауста»: «Не бог ли эти знаки начертал? Таинственен их скрытый дар!..», а также Г. Герца: «Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами и их первооткрыватели, и что мы извлекаем из них больше, чем было в них заложено первоначально» [6, 7].

Ниже будут рассмотрены четыре уравнения системы Максвелла, в которую также входят материальные уравнения (1.5)-(1.7).

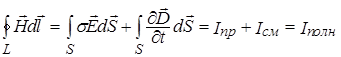. (3.1)

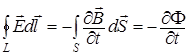. (3.2)

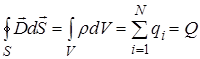. (3.3)

. (3.4)

Первое уравнение Максвелла (3.1) является обобщением закона Био-Савара-Лапласа (I - ток в проводе длиной dl, r - расстояние от оси провода):

, - (3.5)

на случай переменного тока. Закон Био-Савара – результат экспериментальных исследований магнитных полей тонких проводников с током, проведенных Ж. Био и Ф. Саваром в 1820 г., который П. Лаплас сформулировал в виде (3.5) [8].

Для прямолинейного проводника с током 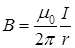. Таким образом, было доказано, что вокруг проводника с током существует магнитное поле, индукция которого (B) пропорциональна силе тока, протекающего в проводнике.

Максвелл предположил, что магнитное поле порождается не только током проводимости, но и током смещения (рис. 3.1.)

В некоторых источниках в качестве основы первого уравнения Максвелла считают закон Ампера, но он определяет силу, действующую на элемент тока:

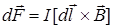. (3.6)

В случае двух прямолинейных параллельных проводников 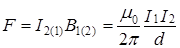, где d - расстояние между проводниками 1 и 2.

Введенный Максвеллом ток смещения – это по существу изменяющееся во времени электрическое поле. Основанием назвать эту величину «током» служит лишь совпадение ее размерности с размерностью тока. Из физических свойств действительного тока ток смещения обладает лишь одним – способностью создавать магнитное поле. Введение тока смещение позволило «уравнять в правах» электрическое и магнитное поля [8].

Сумму тока проводимости и тока смещения называют полным током.

Второе уравнение Максвелла (3.2) является обобщением закона электромагнитной индукции М. Фарадея (левая часть (3.2) – электродвижущая сила, наводимая в контуре L; правая часть (3.2) – изменение во времени магнитного потока). Знак «минус» в правой части соответствует правилу Ленца: «Наведенный ток всегда направлен так, чтобы противодействовать причине, его вызывающей» [8].

Заслуга Максвелла состоит в том, что из закона ЭМ индукции он вывел понятие материального контура: контур не обязательно должен быть проводящим, а может быть воображаемым, проходящим через любые среды, - в этом случае векторы и связаны в точке пространства без участия вещества.

Третье уравнение Максвелла (3.3) является обобщением теоремы Гаусса (левая часть – поток вектора через S, правая часть – полный заряд, заключенный в S, для непрерывного и дискретного распределения заряда). Теорема Гаусса была доказана для электростатического поля. Максвелл постулировал справедливость этого закона для произвольных веществ, зарядов и полей.

Силовые линии электрического поля начинаются и заканчиваются на зарядах – носителях электрического поля (рис. 2.5). При отсутствии электрических зарядов силовые линии электрического поля будут замкнутыми.

Четвертое уравнение Максвелла (3.4) является аналогом теоремы Гаусса для магнитного поля и выражает принцип непрерывности магнитного потока. Входящий и выходящий потоки через S равны. Силовые линии 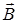замкнуты.

Интегральные уравнения Максвелла верны для физических объектов. Для получения уравнений в дифференциальной форме необходимо осуществить предельный переход, при котором данный объект стягивается в точку.

Дата добавления: 2015-05-10