Радикальный признак Коши

Огюстен Луи Коши – еще более знаменитый французский математик. Биографию Коши вам может рассказать любой студент технической специальности. В самых живописных красках. Не случайно эта фамилия высечена на первом этаже Эйфелевой башни.

Признак сходимости Коши для положительных числовых рядов чем-то похож на только что рассмотренный признак Даламбера.

Радикальный признак Коши: Рассмотрим положительный числовой ряд 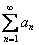. Если существует предел: , то:
а) При ряд сходится. В частности, ряд сходится при .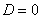
б) При 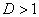ряд расходится. В частности, ряд расходится при .
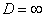в) При 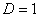признак не дает ответа. Нужно использовать другой признак. Интересно отметить, что если признак Коши не даёт нам ответа на вопрос о сходимости ряда, то признак Даламбера нам тоже не даст ответа. Но если признак Даламбера не даёт ответа, то признак Коши вполне может «сработать». То есть, признак Коши является в этом смысле более сильным признаком.

Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень «хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.

Пример 7

Исследовать ряд на сходимость

Мы видим, что общий член ряда полностью находится под степенью, зависящей от , а значит, нужно использовать радикальный признак Коши:

Таким образом, исследуемый ряд расходится.

(1) Оформляем общий член ряда под корень.
(2) Переписываем то же самое, только уже без корня, используя свойство степеней .
(3) В показателе почленно делим числитель на знаменатель, указывая, что
(4) В результате у нас получилась неопределенность . Здесь можно было пойти длинным путем: возвести в куб, возвести в куб, потом разделить числитель и знаменатель на «эн» в старшей степени. Но в данном случае есть более эффективное решение: можно почленно поделить числитель и знаменатель прямо под степенью-константой. Для устранения неопределенности делим числитель и знаменатель на (старшую степень).
(5) Собственно выполняем почленное деление, и указываем слагаемые, которые стремятся к нулю.
(6) Доводим ответ до ума, помечаем, что и делаем вывод о том, что ряд расходится.

А вот более простой пример для самостоятельного решения:

Пример 8

Исследовать ряд на сходимость

И еще пара типовых примеров.

Полное решение и образец оформления в конце урока

Пример 9

Исследовать ряд на сходимость
Используем радикальный признак Коши:

Таким образом, исследуемый ряд сходится.

(1) Помещаем общий член ряда под корень.
(2) Переписываем то же самое, но уже без корня, при этом раскрываем скобки, используя формулу сокращенного умножения: .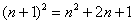
(3) В показателе почленно делим числитель на знаменатель и указываем, что .
(4) Получена неопределенность вида 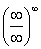. Здесь можно прямо в скобке почленно поделить числитель на знаменатель на «эн» в старшей степени. Нечто подобное у нас встречалось при изучении второго замечательного предела. Но здесь ситуация другая. Если бы коэффициенты при старших степенях были одинаковыми, например: , то фокус с почленным делением уже бы не прошел, и надо было бы использовать второй замечательный предел. Но у нас эти коэффициенты разные (5 и 6), поэтому можно (и нужно) делить почленно (кстати, наоборот – второй замечательный предел при разных коэффициентах при старших степенях уже не прокатывает).
(5) Собственно выполняем почленное деление и указываем, какие слагаемые у нас стремятся к нулю.
(6) Неопределенность устранена, у нас остался простейший предел: 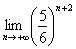. Почему в бесконечно большой степени стремится к нулю? Потому-что основание степени удовлетворяет неравенству . Если у кого есть сомнения в справедливости предела , то я не поленюсь, возьму в руки калькулятор:
Если 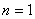, то
Если , то
Если , то
Если , то
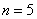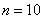Если , то
… и т.д. до бесконечности – то есть, в пределе:
(7) Указываем, что и делаем вывод о том, что ряд сходится.

Пример 10

Исследовать ряд на сходимость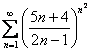

Это пример для самостоятельного решения.

Иногда для решения предлагается провокационный пример, например: . Здесь в показателе степени нет «эн», только константа. Тут нужно возвести в квадрат числитель и знаменатель (получатся многочлены), а далее придерживаться алгоритма из статьи Ряды для чайников. В подобном примере сработать должен либо необходимый признак сходимости ряда либо предельный признак сравнения.

Дата добавления: 2015-05-10