Интегральный признак Коши

Разочарую тех, кто плохо усвоил материал первого курса. Для того чтобы применять интегральный признак Коши необходимо более или менее уверенно уметь находить производные, интегралы, а также иметь навык вычисления несобственного интеграла первого рода.

В учебниках по математическому анализу интегральный признак Коши дан математически строго, но слишком уж поморочено, поэтому я сформулирую признак совсем примитивно, но понятно. И сразу примеры для пояснения.

Интегральный признак Коши: Рассмотрим положительный числовой ряд 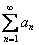. Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.

Пример 11

Исследовать ряд на сходимость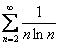

Почти классика. Натуральный логарифм и какая-нибудь бяка.

Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда есть некоторая функция и её производная. Из темы Производная вы наверняка запомнили простейшую табличную вещь: 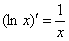, и у нас как раз такой канонический случай.

Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: 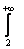. Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»: 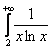. Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала: .

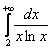Теперь нужно вычислить несобственный интеграл 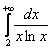. При этом возможно два случая:

1) Если выяснится, что интеграл 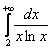сходится, то будет сходиться и наш ряд .

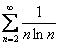2) Если выяснится, что интеграл 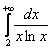расходится, то наш ряд 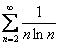тоже будет расходиться.

Повторюсь, если материал запущен, то чтение параграфа будет трудным и малопонятным, поскольку применение признака по сути дела сводится к вычислению несобственного интеграла первого рода.

Полное решение и оформление примера должно выглядеть примерно так:

Используем интегральный признак:

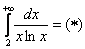
Подынтегральная функция непрерывна на

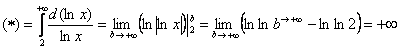
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.

Пример 12

Исследовать ряд на сходимость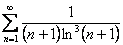

Решение и образец оформления в конце урока

В рассмотренных примерах логарифм также мог находиться под корнем, это не изменило бы способа решения.

И еще два примера на закуску

Пример 13

Исследовать ряд на сходимость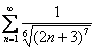

По общим «параметрам» общий член ряда вроде бы подходит для использования предельного признака сравнения. Нужно всего лишь раскрыть скобк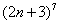и и сразу сдать на кандидата предельно сравнить данный ряд со сходящимся рядом 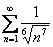. Впрочем, я немного слукавил, скобки можно и не раскрывать, но всё равно решение через предельный признак сравнения будет выглядеть довольно вычурно.

Поэтому мы используем интегральный признак Коши:

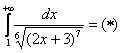
Подынтегральная функция непрерывна на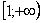

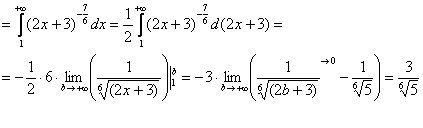
Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.

! Примечание: полученное число – не является суммой ряда!!!

Пример 14

Исследовать ряд на сходимость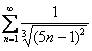

Решение и образец оформления в конце урока, который подходит к концу.

Да. Возможно, у некоторых возник вопрос, почему я начал этот урок с таким энтузиазмом? Всё просто – начался учебный год, а мне не нужно на учебу!!! Я столько мучался =(Что даже не устал в заключительных аккордах этой статьи.

В целях окончательного и бесповоротного усвоения темы числовых рядов посетите урок Знакочередующиеся ряды. Признак Лейбница. Примеры решений.

Желаю успехов!

Решения и ответы:

Пример 3: Используем признак Даламбера:

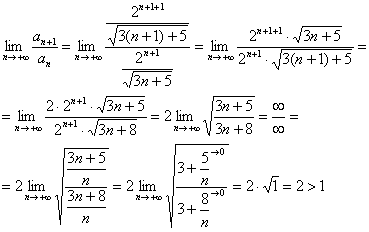
Таким образом, исследуемый ряд расходится.
Примечание: Можно было использовать и «турбо»-метод решения: сразу обвести карандашом отношение 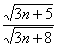, указать, что оно стремится к единице и сделать пометку: «одного порядка роста».

Пример 5: Используем признак Даламбера:

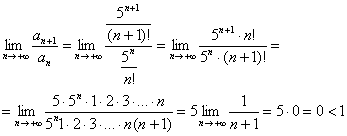
Таким образом, исследуемый ряд сходится.

Пример 8:
Используем радикальный признак Коши.

Таким образом, исследуемый ряд сходится.

Пример 10:
Используем радикальный признак Коши.

Таким образом, исследуемый ряд расходится.
Примечание: Здесь основание степени 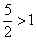, поэтому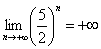

Пример 12:
Используем интегральный признак.

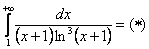
Подынтегральная функция непрерывна на .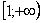

Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.

Пример 14:
Используем интегральный признак.

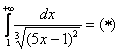
Подынтегральная функция непрерывна на .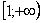

Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Примечание: Ряд 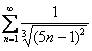также можно исследовать с помощью предельного признака сравнения. Для этого необходимо раскрыть скобки под корнем 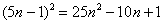и сравнить исследуемый ряд с расходящимся рядом .

Автор: Емелин Александр

Дата добавления: 2015-05-10