Процесс гибели и размножения

Телефон: [phone]

МЫ ВАС ЖДЕМ СПА-КОСМЕТОЛОГИИ «КОНСОЛЬ» 4 ЭТАЖ! С 9.00 ДО 21.00 ЕЖЕДНЕВНО

ПРИ ПОКУПКЕ 10 ПРОЦЕДУР(КУРС)-10%

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

λ₁₂

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 1.

Рассмотрим упорядоченное множество состояний системы S₀, S₁, S₂,…S_k. Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния S_k возможны переходы только либо в состояние S_k-1, либо в состояние S_k+1[1]_.

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями λ_k,k+1 или λ_k+1,k.

По графу, представленному на рис. 1, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений получим: для состояния S₀

, (1)

для состояния S₁ - , которое с учетом (1) приводится к виду

. (2)

Аналогично, записывал уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

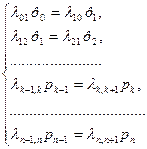(3)

к которой добавляется нормировочное условие

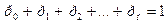. (4)

Решим эту систему. Для этого выразим все переменные через .

Из первого уравнения выразим :

. (*)

Из второго, с учетом предыдущего равенства, получим

. (**)

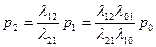И так далее. Общая формула имеет вид:

. (***)

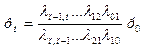Формулы (*) – (***) обозначим цифрой (5).

Все вероятности выражены через одну из них: . Подставив эти выражения в нормировочное условие и вынося , получим:

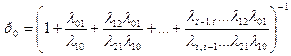, (6)

Заметим, что в формулах (5) для р ₁, р ₂,…, р_п коэффициенты при р ₀ есть слагаемые, стоящие после единицы в формуле (6). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния S_k (k = 1, 2, …, n), а знаменатели – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния S_k.

Пример 1. Процесс гибели и размножения представлен графом (рис. 2). Найти предельные вероятности состояний.

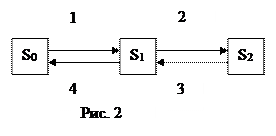
Решение. По формуле (6)найдем

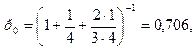по (5) - , , т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии S₀, 17,6% — в состоянии S₁ и 11,8% — в состоянии S₂.

Дата добавления: 2015-05-10