Краткая теория. Вопросы к защите лабораторной работы

МЕТОД КРУТИЛЬНОГО БАЛЛИСТИЧЕСКОГО МАЯТНИКА

РАБОТА 1

Литература.

Вопросы к защите лабораторной работы.

· Электрический двигатель как объект управления. Управляющие и возмущающие воздействия. Выходные переменные.

· Регулировочные и нагрузочные характеристики двигателя.

· Понятия цели, управления, регулирования и ошибки системы.

· В чем заключается цель управления двигателем постоянного тока?

· Как решается задача достижения цели в разомкнутой, статической и комбинированной системах?

· Что такое статическая ошибка? От чего она зависит? Как её уменьшить?

· Понятие статизма и астатизма. Расчет статизма.

· Чем отличаются:

· структурные схемы,

· принципиальные схемы,

· передаточные функции,

· нагрузочные характеристики,

· статические ошибки,

· управляющие устройства - регуляторы

изучаемых систем регулирования?

1. Лабораторные работы по курсу «Основы теории автоматического управления». О. С. Колосов, С.А. Хризолитова. – М.: Изд – во МЭИ, 1964.–30 с.

2. Петрова В. А., Ягодкина Т. В. Математическое описание линейных непрерывных систем автоматического управления. - М.: МЭИ, 1992. -103 с.

ЦЕЛЬ РАБОТЫ: определить скорость полета пули при помощи крутильного баллистического маятника.

ОБОРУДОВАНИЕ: крутильный баллистический маятник, пружинный пистолет, осветитель, масштабная линейка.

Экспериментальная установка состоит из крутильного баллистического маятника и пистолета (рис. 1).

Крутильный маятник собран из двух массивных металлических стержней (1), скрепленных муфтой (2).

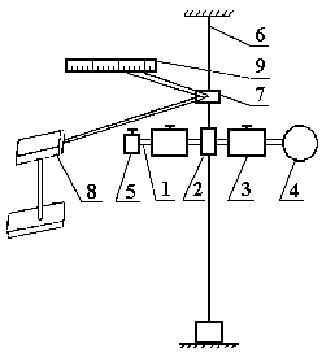
Рис.1 Схема установки

1 – стержень, 2 – муфта, 3 – груз, 4 – мишень,

5 – противовес, 6 – проволока/растяжка, 7 – зеркальце,

8 – осветитель, 9 – шкала.

По горизонтальному стержню могут перемещаться два металлических цилиндра (груза) (3). На одном конце стержня находится мишень (4) для пули, на противоположном – противовес (5) для уравновешивания мишени. Маятник укреплен на кронштейне при помощи проволоки (6), деформация которой создает момент упругости сил и подшипника. Для измерения угла поворота маятника на нем укреплено зеркальце (7). Луч от осветителя (8), отражается от зеркальца, скользит по шкале (9).

Пистолет представляет собой металлическую трубку – ствол, укрепленную на штативе. В закрытом конце этой трубки имеется пружина. Пружина сжимается, пуля помещается в ствол. После освобождения пружины пуля выбрасывается.

После попадания пули в маятник он начнет колебаться вокруг своей вертикальной оси. Если пренебречь при его движении моментом сил трения, то можно воспользоваться двумя законами сохранения.

На основании закона сохранении момента импульса, считая удар полностью неупругим, можно написать (до удара и после удара):

mvl = (I₁ + ml²)w,

где m – масса пули,

v – ее скорость,

l – расстояние от оси вращения маятника, до точки удара пули,

w - угловая скорость маятника,

I₁ – момент инерции маятника.

Закон сохранения механической энергии (после удара) дает

0,5(I₁+ ml²)w²=0,5Dj², (2)

где j - угол (наибольший) поворота маятника,

D – постоянная момента упругих сил.

Из этих уравнений получаем

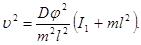(3)

Так как момент инерции пули ml² во много раз меньше I₁, то уравнение (3) может быть написано в виде:

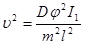(4)

Рассмотрим условия колебания маятника. Будем считать, что:

1) t<<T, т.е. время воздействия пули на маятник во много раз меньше периода колебаний маятника (баллистический маятник),

2) sin(a)» a, т.е. угол отклонения маятника мал – не более 5°-6°

Уравнение движения баллистического маятника при этих условиях может быть написано в виде:

,

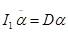где a — угол поворота маятника, — угловое ускорение.

Решение этого уравнения приводит к выражению для периода колебаний

. (5)

Для исключения величины D можно поступить следующим образом. Изменим момент инерции маятника, изменив расстояние между грузами. Тогда:

(6)

, (7)

Где T₂ – период колебаний при новом значении момента инерции I₂,

DI – разность моментов инерции.

Уравнения (6) дают

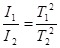, (8)

Из уравнений (7) и (8) получаем

(9)

Уравнения (4), (5), (9) дают

(10)

Величину DI можно определить, пользуясь теоремой Штейнера. Из этой теоремы следует, что

(11)

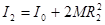, (12)

где I₀ – момент инерции маятника, когда центры тяжести грузов совпадают с осью вращения маятника,

I₁ – момент инерции, когда оба груза находятся на расстоянии R₁ от оси вращения,

I₂ – момент инерции, когда оба груза находятся на расстоянии R₂,

M – масса одного груза.

Пусть R₁>R₂, тогда из уравнений (11) и (12) получаем

. (13)

Величина угла поворота j определяется с учетом закона отражения луча

, (14)

где L – расстояние от зеркальца до «зайчика» на шкале,

n – число делений шкалы, на которое смещается зайчик.

Из уравнения (10), (13), (14) получите расчетную формулу.

Дата добавления: 2015-05-10