Краткая теория

РАБОТА 2

ИЗМЕРЕНИЯ

Масса грузов известна и равна (в большой установке) М = 1625 г.

Начинают с того, что оба цилиндра раздвигают вдоль стержня на некоторое расстояние R₁ от оси маятника и измеряют это расстояние (R₁ — расстояние между осью маятника и серединой цилиндра). Измерьте также l — расстояние между осью маятника и серединой мишени. Затем установите правильно расположение зеркальца, маятника и пистолета так, чтобы:

1) расстояние L было наименьшим;

2) ось ствола пистолета была перпендикулярна к оси горизонтального стержня маятника; ось ствола и ось стержня были в одной горизонтальной плоскости;

3) конец ствола пистолета был на расстоянии 15—20 см от мишени.

Расстояние между зеркальцем и «зайчиком» измерьте сантиметровой линейкой. После этого произведите выстрел и отсчитайте величину n, т.е. наибольшее отклонение «зайчика» от положения равновесия.

Для измерения периода колебания Т₁ пустите в ход секундомер, не останавливая маятника. Через десять полных колебаний секундомер остановите, определите среднее арифметическое значение величины периода. Уменьшив момент инерции маятника (придвинув цилиндры вплотную к муфте), измерьте расстояние между осью маятника и серединой одного из цилиндров.

Для измерения периода колебания Т₂ снова произведите «выстрел» (измерять отклонение «зайчика» по шкале не следует). Определение величины периода Т₂ производится так же, как и величинаТ₁.

По расчетной формуле определите скорость пули. Изменяя расстояние R₁, проведите еще 7 — 8 измерений величины скорости пули, рассчитайте абсолютную ошибку (как для косвенного измерения). Результаты измерений и их обработку оформите в виде таблицы (составьте самостоятельно).

Контрольные вопросы

1) Можно ли пользоваться приведенной теорией, если удар пули о мишень происходит под углом, отличным от прямого?

2) Какие факты могут влиять на точность эксперимента? (Отразите это в выводе по работе)

3) При каких упрощающих предположениях развита теория опыта?

МЕТОД БАЛЛИСТИЧЕСКОГО МАЯТНИКА И МЕТОД ВРАЩАЮЩИХСЯ ДИСКОВ

ЦЕЛЬ РАБОТЫ: определение скорости движения пули кинематическим и динамическим методом.

ОБОРУДОВАНИЕ: пневматическое ружье на стойке, пули, прибор Поля, баллистический маятник, бумажные диски, тахометр, шкала, линейка.

Кинематический метод определения скорости движения пули является прямым методом и основан на измерении времени, в течение которого пуля пролетает известное расстояние между двумя равномерно вращающимися бумажными дисками.

Прибор Поля представляет собой два тонких бумажных диска, закрепленных на общей оси, на некотором расстоянии друг от друга. Ось приводится во вращение мотором (рис.2).

Пуля, направленная параллельно оси вращения, пробивает оба диска. За время полёта пули между дисками последние успевают повернуться на некоторый угол 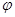, так, что пробоины не лежат на линии, параллельной оси вращения. По смещению пробоин, которое удобно измерить, сдвинув диски вдоль оси до соприкосновения, можно определить скорость полёта пули. Скорость вращения мотора определяется с помощью тахометра или по паспортным данным мотора.

Расчетную формулу для определения скорости пули выведите самостоятельно.

Динамический метод определения скорости движения пули является косвенным и основан на использовании (в общем случае) закона сохранения импульса.

Баллистический маятник представляет собой тяжелое тело (массы М), подвешенное на двойном бифилярном подвесе (рис. 2). Горизонтально летящая пуля массы m попадаетна маятник и застревает в нём (абсолютно неупругий удар). Если время t соударения пули с маятником мало по сравнению с периодом Т колебания маятника, то маятник не успевает заметно отклониться от исходного положения за время соударения. Это, значит, что во время удара не возникает силы, стремящейся вернуть маятник в исходное положение. Поэтому такую систему «снаряд-маятник» можно рассматривать как замкнутую и применять в ней закон сохранения импульса и момента импульса.

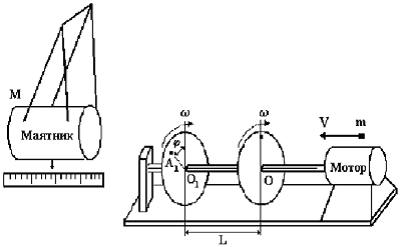
Рис. 2. Схема установки

В условиях нашей задачи t<<T, следовательно, можно написать

mu = (M+m)V. (15)

(до удара) (после удара)

Применение в нашем случае к удару пули о маятник закона сохранения импульса в системе “снаряд-маятник” является вполне допустимым приемом решения данной задачи, но совсем не универсальным для задач о соударении двух твердых тел, из которых одно имеет неподвижную ось вращения.

Возможность использования закона сохранения импульса связана в данном случае с тем, что размеры маятника малы по сравнению с длиной нити подвеса, т.е. данный маятник можно рассматривать как математический, и тогда, как легко показать, что уравнение, выражающее закон сохранения момента импульса, переходит в уравнение, выражающее закон сохранения импульса.

Действительно, закон сохранения момента импульса для системы “пуля-маятник” запишется в виде

lmu =Iw, (16)

где mlu — момент импульса пули до удара;

I — момент инерции маятника с пулей относительно оси вращения, проходящей через точку подвеса (с угловой скоростью

w = V/l)

I = (M+m)l²

(l — расстояние от центра тяжести системы «маятник-пуля» до точки подвеса). Подставляя это значение I в формулу (16), получим

mu l = (M+m)l²V/l

или

mul = (M+m)V,

т.е соотношение, выражающее закон сохранения импульса.

Снизу маятника укреплено острие-указатель, которое при отклонении маятника перемещается вдоль шкалы, и позволяет фиксировать наибольшее отклонение маятника от положения равновесия.

Так как масса пули мала по сравнению с массой маятника, то уравнение (15) можно переписать в виде

mu = M V

и скорость пули

u = 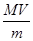. (17)

Скорость маятника V можно определить, использовав закон сохранения энергии. Получив в момент удара кинетическую энергию mV²/2 маятник отклоняется от положения равновесия, поднимаясь при этом на некоторую высоту h. В крайнем положении, когда маятник на мгновение остановится, прирост его потенциальной энергии равен начальной кинетической энергии, полученной им в момент удара

Mgh = 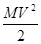(18)

откуда V = 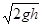(19)

Непосредственное измерение h затруднительно ввиду ее малости, но h можно выразить через длину подвеса маятника L и отклонение маятника по горизонтали S. Из треугольника АОВ (рис.3) определим величину h: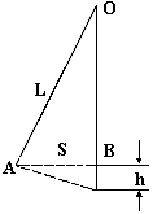

S² + (L-h)² = L²,

откуда S² = 2Lh - h².

В условиях опыта h<<L, поэтому величиной h² можно пренебречь по сравнению с 2Lh, следовательно,

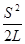h = (20)

Теперь легко получить окончательную формулу для расчета скорости полета пули. Сделайте это.

Дата добавления: 2015-05-10