Расчетно-графическая работа №9

Эпюры поперечных сил и изгибающих моментов. Расчеты на прочность при прямом поперечном изгибе.

Задание 1. Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавра и прямоугольника с соотношением сторон h=2b. Материал балки – сталь, допускаемое напряжение [σ] = 160 МПа. Рассчитать площади поперечных сечений и сделать вывод о целесообразности применения сечения данной формы.

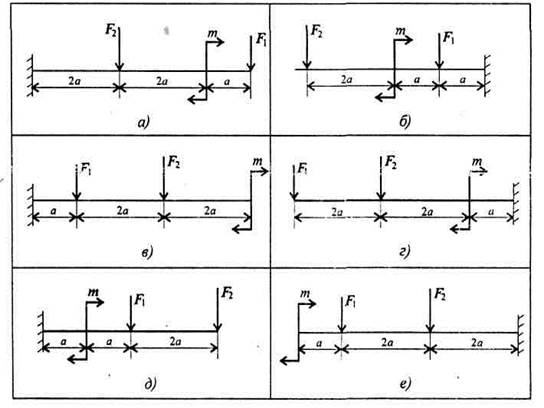
Параметр	Вариант
F1, кН
F2, кН	4,4	4,8	7,8	8,4		12,8			22,8
m, кН·м
a, м	0,2	0,2	0,3	0,3	0,4	0,4	0,5	0,5	0,6	0,6

Указания по выполнению задания.

1. Изобразить выбранную расчетную схему балки с приложенной к ней нагрузкой.

2. Разделить балку на участки и, используя метод сечений и правила построения эпюр поперечных сил и изгибающих моментов, построить эти эпюры под расчетной схемой балки.

3. Определить максимальный изгибающий момент и, используя условие прочности при прямом поперечном изгибе, выполнить проектировочный расчет (рассчитать момент сопротивления изгибу).

4. По ГОСТ 8239-89 подобрать размер двутавровой балки по рассчитанному моменту сопротивления изгибу и определить площадь ее поперечного сечения.

5. Используя формулу момента сопротивления изгибу прямоугольного сечения и заданное соотношение сторон этого сечения, рассчитать размер такого сечения и его площадь.

6. Сравнить величины площадей поперечных сечений двутавровой и прямоугольной балок и сделать вывод о целесообразности применения сечения данной формы (с точки зрения материалоемкости).

Задание 2. Для двухопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и, используя условие прочности, подобрать для данной балки необходимый размер швеллера. Материал – сталь, допускаемое напряжение [σ]=160 МПа.

Параметр	Вариант
F1, кН
F2, кН	4,4	4,8	7,8	8,4		12,8			22,8
m, кН·м
a, м	0,2	0,2	0,3	0,3	0,4	0,4	0,5	0,5	0,6	0,6

Указания по выполнению задания.

1. Изобразить выбранную расчетную схему балки с приложенной к ней нагрузкой.

2. Составить уравнения равновесия ∑ F_iy=0; ∑ F_ix=0; ∑ M_i=0 и определить величину и направление опорных реакций балки.

3. Разделить балку на участки и, используя метод сечений и правила построения эпюр поперечных сил и изгибающих моментов, построить эти эпюры под расчетной схемой балки (при расчетах учитывать опорные реакции).

4. Определить максимальный изгибающий момент и, используя условие прочности при прямом поперечном изгибе, выполнить проектировочный расчет (рассчитать момент сопротивления изгибу).

5. По ГОСТ 8240-89 подобрать размер швеллерной балки по рассчитанному моменту сопротивления изгибу.

Задание3. Для двухопорной консольной балки, нагруженной сосредоточенными силами, парой сил с моментом m и распределенной нагрузкой интенсивностью q, построить эпюры поперечных сил и изгибающих моментов.

Проверить прочность балки. В случае, если прочность не обеспечена, подобрать сечение большего размера. Материал – сталь, допускаемое напряжение изгиба

[σ] =160 МПа. Сечение балок – сдвоенный двутавр.

В вариантах 1-5 используется двутавр №20.

В вариантах 6-10 – двутавр №30.

Параметр	Вариант
m, кН·м
F, кН
q, кН/м
a, м	0,5	0,6	0,8	0,9			1,1	0,9	0,6	0,8
b, м	1,5	1,6	1,8	1,9			2,3	2,1	2,5	2,3
c, м	1,5	1,7	1,9		2,1	1,8	2,7	2,5	2,6	2,4

Указания по выполнению задания.

1. Изобразить выбранную расчетную схему балки с приложенной к ней нагрузкой.

2. Составить уравнения равновесия ∑ F_iy=0; ∑ F_ix=0; ∑ M_i=0 и определить величину и направление опорных реакций балки.

3. Разделить балку на участки и, используя метод сечений и правила построения эпюр поперечных сил и изгибающих моментов, построить эти эпюры под расчетной схемой балки.

4. Определить по эпюре максимальный изгибающий момент и по ГОСТ 8239-89 - момент сопротивления изгибу двутавровой балки.

5. Учитывая, что балка сдвоенная, выполнить проверочный расчет на прочность.

6. Если балки заданного размера не обеспечивают прочность конструкции, подобрать по ГОСТ 8239-89 другой размер балок.

Последовательность построения эпюр поперечных сил

и изгибающих моментов по уравнениям.

1. Определить опорные реакции, решая систему уравнений равновесия ∑ F_iy=0; ∑ F_ix=0; ∑ M_i=0,и проверить найденные значения.

2. Балку разделить на участки, границы которых определяются точками приложения сил, пар сил или точками начала и конца распределенной нагрузки.

3. На каждом участке мысленно проводить поперечное сечение и, рассматривая равновесие отсеченной части балки (правой или левой), составить уравнения зависимости поперечной силы и изгибающего момента от абсциссы (длины) оси балки.

4. Подставляя значения абсциссы в граничных, экстремальных и других характерных точках на каждом участке балки, вычислить величины поперечных сил и изгибающих моментов в этих точках.

5. По полученным величинам поперечных сил и изгибающих моментов построить в выбранном масштабе соответствующие эпюры.

Последовательность построения эпюр поперечных сил

и изгибающих моментов по характерным точкам.

1. Определить опорные реакции, решая систему уравнений равновесия ∑ F_iy=0; ∑ F_ix=0; ∑ M_i= 0, и проверить найденные значения.

2. Балку разделить на участки, границы которых определяются характерными точками, то есть точками приложения сил, пар сил или точками начала и конца распределенной нагрузки.

3. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки.

4. Рассчитать поперечные силы в сечениях, проходящих через характерные точки (характерных сечениях), и построить эпюру.

5. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки.

6. Рассчитать изгибающие моменты в характерных сечениях и построить эпюру.

Дата добавления: 2015-05-10