Обработка ведомости вычисления координат вершин теодолитного хода

Указания к выполнению работы

1.1 Увязка углов теодолитного хода. В ведомости вычисления координат записывают исходный дирекционный угол _1.

Вычисляют сумму измеренных углов хода _пр . Определяют теоретическую сумму углов

, (1)

где n – количество углов.

Находят угловую невязку

(2)

Если невязка не превышает предельно-допустимой величины

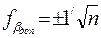, (3)

то ее распределяют с обратным знаком поровну на все углы хода, с округлым значением поправок до десятых долей минут. Исправленные этими поправками углы записывают в ведомости. Сумма исправленных углов должна равняться теоретической сумме углов.

1.2 Вычисление дирекционных углов и румбов сторон хода.

По исходному дирекционному углу ₁ и исправленным значениям углов 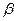хода по формуле для правых углов вычисляют дирекционные углы всех остальных сторон: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180 и минус правый (исправленный) угол хода, образованный этими сторонами.

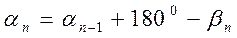(4)

Вычисления дирекционных углов контролируются получением в конце значения дирекционного угла стороны 1 – 2 ( ₁ ).

Примечание. Если дирекционный угол больше 360 , то из него вычитают 360 .

1.3 Определение румбов сторон теодолитного хода.

По дирекционным углам, пользуясь таблицей 1, вычисляют соответствующие румбы.

Таблица 1 – Соотношение между румбами и дирекционными углами.

Значение дирекционных углов записывают в ведомости.

1.4 Вычисление приращений координат.

Приращения координат вычисляют по румбам и горизонтальным проложениям линий по следующим формулам

(5)

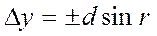(6)

Приращения координат вычисляют по таблицам натуральных величин тригонометрических функции или на микрокалькуляторе.

Вычисленные значения приращений и записывают в ведомости с точностью до сотых долей метра. Знаки приращений устанавливают по названию румба, пользуясь таблицей 1.

Таблица 1. Зависимость между дирекционными углами и румбами

Интервал изменения дирекционных углов	Название румбов	Зависимость между дирекционными углами и румбами	Знаки приращений координат
	СВ		+	+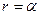
	ЮВ		–	+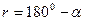
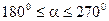
	ЮЗ		–	–
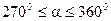
	СЗ		+	–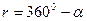

Контролем правильности вычисления приращения координат является формула

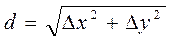(7)

1.5 Определение невязок в приращениях координат.

Теоретически алгебраическая сумма приращений координат по осям абсциссы и ординат должна быть равна нулю, но результаты измерений линий содержат ошибки, вследствии которых практически возникают невязки.

(8)

(9)

Величины и 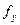называются линейными невязками в приращениях координат соответственно по оси абсцисс и по оси ординат

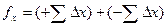(10)

(11)

1.6 Полученные невязки сравнивают с предельно-допустимыми величинами погрешностей.

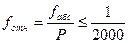(12)

где ; (13)

Р – периметр теодолитного хода.

Если 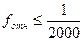, то полученные ƒx и ƒy считаются допустимыми.

1.7 Вычисление поправок.

Поправки вычисляют по следующим формулам:

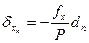(14)

(15)

Примечание: если полученные невязки находятся в пределах [0,01-0,04], то поправки не вычисляются.

1.8 Определение исправленных приращений координат.

С учетом поправок исправляют вычисленные приращения координат

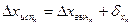; (16)

Примечание: невязки находящиеся в пределах [0,01-0,04] вводятся в пятое приращение координат, с обратным знаком невязок.

1.7 Определение координат точек.

По условным координатам первой точки и исправленным приращениям координат вычисляют координаты всех вершин полигона.

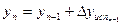; (17)

Координата последующей точки равна координате предыдущей точки плюс исправленное приращение координат.

Дата добавления: 2015-05-10