Основные понятия. Системы и модели массового обслуживания

Системы и модели массового обслуживания

Менеджеру-экономисту приходится сталкиваться с ситуациями, которые характеризуются термином системы массового обслуживания. Пример

1. обслуживание покупателей в сфере розничной торговли

2. транспортное обслуживание

3. медицинское обслуживание населения

4. ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации

5. обработка документов в системе управления

6. туристическое обслуживание

(билетные кассы, справочные бюро, телефонные станции)

Главная особенность процессов массового обслуживания – случайность. ТМО опирается на теорию вероятностей и математическую статистику.

Первоначально развитие теории массового обслуживания связано с именем датского ученого А.К.Эрланга (1878-1929), с его трудами в области проектирования и эксплуатации телефонных станций. Большой вклад в развитие этой теории внесли российские математики А.Я.Хинчин, Б.В.Гнеденко, А.Н.Колмогоров, Е.С. Вентцель и др.

Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания. В качестве каналов могут фигурировать технические устройства либо персонал, выполняющие функции обслуживания. Различают однофазные и многофазные каналы. При однофазном канале весь процесс обслуживания от начала до конца выполняется либо 1-м техническим устройством, либо 1-м человеком.

В зависимости от числа каналов системы массового обслуживания могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих на СМО в какие-то, вообще говоря, случайные моменты времени. Обслуживание поступившей заявки продолжается некоторое (вообще говоря, случайное) время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких систем массового обслуживания, процесс функционирования которых является марковским, то есть все потоки событий, переводящие систему из состояния в состояние, простейшие.

Простейший поток обладает тремя основными свойствами: стационарности, ординарности и отсутствия последствия.

Свойство стационарности обеспечивает постоянное количество требований в течение некоторого промежутка. При этом количество требований зависит только от дины этого промежутка по оси времени, т.е. это свойство не учитывает суточные и годовые колебания спроса.

Свойство ординарности указывает, что вероятность поступления 2х заявок одновременно является бесконечно малой величиной.

Свойство отсутствия последствия состоит в том, что количество требований, поступивших в систему после времени t₀ не зависит от числа требований до этого момента.

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t ровно k требований задается формулой

,

- плотность потока или среднее число требований в единицу времени.

Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, а также от характера потока заявок, обладает какой-то пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок.

Предмет теории массового обслуживания — установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания.

КЛАССИФИКАЦИЯ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ И ИХ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ

Системы массового обслуживания (СМО) классифицируются по разным признакам.

В зависимости от условий ожидания требованием начала обслуживания различают СМО с отказами и СМО с ожиданием.

Системы массового обслуживания вообще могут быть двух типов.

1. Системы с отказами. В таких системах заявка, поступившая в момент, когда все каналы заняты, получает «отказ», покидает СМО и в дальнейшем процессе обслуживания не участвует.

2. Системы с ожиданием (с очередью). В таких системах заявка, поступившая в момент, когда все каналы заняты, становится в очередь и ожидает, пока не освободится один из каналов. Как только освободится канал, принимается к обслуживанию одна из заявок, стоящих в очереди.

Для систем с ожиданием важна дисциплина очереди. Под дисциплиной очереди понимается порядок, который принят при поступлении требований из очереди в канал обслуживания.

Различают следующие виды дисциплины очереди:

упорядоченное обслуживание:

первый пришел – первый обслуживается(английская аббревиатура FIFO – First Input First Output);

последний пришел – первый обслуживается (английская аббревиатура LIFO – Last Input First Output);

неупорядоченное обслуживание:

заявки попадают в канал обслуживания случайным образом;

с приоритетами:

при которой некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания.

Системы с очередью делятся на системы с неограниченным ожиданием и системы с ограниченным ожиданием.

В системах с неограниченным ожиданием каждая заявка, поступившая в момент, когда нет свободных каналов, становится в очередь и «терпеливо» ждет освобождения канала, который примет ее к обслуживанию. Любая заявка, поступившая в СМО, рано или поздно будет обслужена.

В системах с ограниченным ожиданием на пребывание заявки в очереди накладываются те или другие ограничения. Эти ограничения могут касаться длины очереди (числа заявок, одновременно находящихся в очереди), времени пребывания заявки в очереди (после какого-то срока пребывания в очереди заявка покидает очередь и уходит), общего времени пребывания заявки в СМО и т. д.

В зависимости от типа СМО, при оценке ее эффективности могут применяться те или другие величины (показатели эффективности).

Например, для СМО с отказами одной из важнейших характеристик является так называемая абсолютная пропускная способность — среднее число заявок, которое может обслужить система за единицу времени.

Наряду с абсолютной, часто рассматривается относительная пропускная способность — средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок).

Помимо абсолютной и относительной пропускной способностей, при анализе СМО с отказами нас могут, в зависимости от задачи исследования, интересовать и другие характеристики, например:

— среднее число занятых каналов,

— среднее относительное время простоя системы в целом и отдельного канала и т. д.

Перейдем к рассмотрению характеристик СМО с ожиданием.

Очевидно, для СМО с неограниченным ожиданием как абсолютная, так и относительная пропускная способность теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Зато для такой СМО весьма важными характеристиками являются:

— среднее число заявок в очереди,

— среднее число заявок в системе (в очереди и под обслуживанием),

— среднее время ожидания заявки в очереди,

— среднее время пребывания заявки в системе (в очереди и под обслуживанием),

и другие характеристики ожидания.

Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик: как абсолютная и относительная пропускная способности, так и характеристики ожидания.

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n, интенсивность потока заявок l, производительность каждого канала (среднее число заявок m, обслуживаемое каналом в единицу времени), условия образования очереди (ограничения, если они есть).

В зависимости от этих параметров мы и будем в дальнейшем выражать характеристики эффективности работы СМО.

Заранее условимся (чтобы не оговаривать это всякий раз отдельно), что мы будем считать все потоки событий, переводящие СМО из состояния в состояние, пуассоновскими.

По месту нахождения источника требований СМО делятся на разомкнутые (когда источник требований находится вне системы) и замкнутые (когда источник находится в самой системе).

Многоканальная СМО с ожиданием. Пусть в n-канальную систему массового обслуживания поступает простейший поток требований с интенсивностью λ; число мест в очереди ограничено и равно т. Время обслуживания требований (для одного канала) экспоненциальное, со средним значением t_обс

Размеченный граф состояний системы представлен на рисунке.

Используем общепринятое обозначение относительной нагрузки на систему

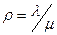
Предельные вероятности состояний системы имеют вид

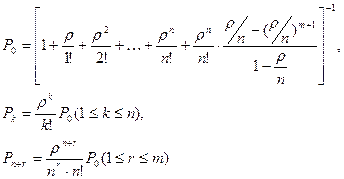
Требование получает отказ в том случае, когда система занята, то есть вероятность отказа

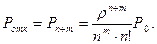
Относительная пропускная способность или вероятность того, что поступившее в систему требование будет принято к обслуживанию, дополняет вероятность отказа до единицы

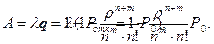В систему поступает λ требований в единицу времени, а доля требований, принятых к обслуживанию, равна q. Следовательно, абсолютная пропускная способность

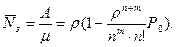Каждый канал, если он занят, обслуживает в единицу времени λтребований, а вся система —А требований. Таким образом, среднее число занятых каналов

Среднее число требований, находящихся в очереди, вычислим как математическое ожидание числа требований, находящихся в очереди:

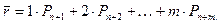
Подставив значения Р_n+r(r= 1, m) и выполнив преобразования, окончательно получим

Учитывая, что среднее число требований, находящихся под обслуживанием, совпадает со средним числом занятых каналов, среднее число требований, находящихся в системе, равно

Среднее время пребывания требований в очереди

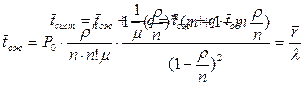Среднее время пребывания требования в системе получим, если к среднему времени ожидания в очереди прибавим среднее время обслуживания, умноженное на относительную пропускную способность q

Многоканальная СМО с неограниченной длиной очереди. Так как длина очереди не ограничена, то граф состояний в этом случае является бесконечным

Установившийся режим работы системы существует при 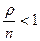, а при 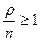очередь будет расти неограниченно. Полагаем, что 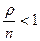. Формулы для расчета характеристик СМО с неограниченной очередью. Предельные вероятности состояний:

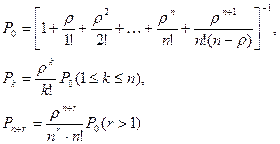
Так как число мест в очереди не ограничено, то все требования, поступившие в систему, рано или поздно будут обслужены. Следовательно

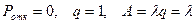
Среднее число занятых каналов

Среднее число требований, находящихся в очереди

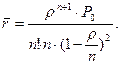
Среднее число требований, находящихся в системе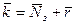

Среднее время пребывания требования в очереди

Среднее время пребывания требования в системе

Многоканальная СМО с отказами. Если требование поступает в систему в момент, когда все п каналов заняты, то оно получает отказ (покидает систему не обслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца. Размеченный граф состояний системы с отказами представлен на рисунке.

Предельные вероятности состояний системы (формулы Эрланга) для рассматриваемой СМО имеют вид

Вероятность отказа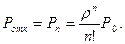

Относительная пропускная способность

Абсолютная пропускная способность A=λq

Среднее число занятых каналов

Дата добавления: 2015-05-10