Знакоопределенность квадратичной формы

Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

>0 ( <0).

Например, квадратичная форма 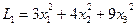является положительно определенной, а форма – отрицательно определенной.

Положительно и отрицательно определенные квадратичные формы имеют общее название «знакоопределенные квадратичные формы». Если квадратичная форма принимает как положительные, так и отрицательные значения, то она называется знакопеременной.

Теорема. Для того, чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 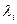матрицы А были положительны (отрицательны).

Теорема (критерий Сильвестра). Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы[1] этой формы были положительны, т.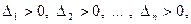е. где

.

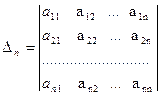Замечание. Для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка, т.е. миноры нечетного порядка отрицательны, а четного – положительны.

Пример. Доказать, что квадратичная форма 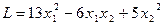является положительно определенной.

Решение.

Первый способ. (с помощью собственных значений матрицы):

?

.

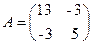
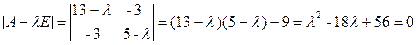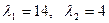Так как оба собственных значения положительны, то квадратичная форма L положительно определенная.

Первый способ (критерий Сильвестра):

.

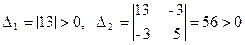Оба главных минора положительны, следовательно, квадратичная форма положительно определенная.

[1] Главные миноры матрицы – это всевозможные миноры, построенные на ее главной диагонали.

Дата добавления: 2015-05-10