Кроме того

Этапы математического моделирования

В процессе построения математической модели можно выделить ряд взаимосвязанных этапов:

1 этап: Постановка задачи. Формулируется цель запланированного исследования, ставятся задачи, проводится качественное описание объекта.

2 этап: Определение задачи и построение описательной (концептуальной) модели. Исследователь определяет, к какому виду относится объект, описывает параметры состояния объекта, переменные, характеристики, факторы внешней среды.

3 этап: Составление математической модели. Изучаемый объект описывается с помощью математической модели, определяются методы ее исследования.

4 этап: Работа с математической моделью. Решение задачи на базе разработанной модели, определение оптимального решения математическими методами.

5 этап: Анализ полученного решения. Установление соответствия построенной математической модели описываемому экономическому процессу.

6 этап: Формулировка выводов. Представление результатов решения в форме удобной для изучения, анализ полученных результатов, формулировка выводов. Результат, полученный при исследовании экономического процесса, должен быть экономически интерпретирован и всесторонне проанализирован.

Итак, решения y ₁ и y ₂ образуют фундаментальную систему и общее ре-

шение в этом случае имеет вид

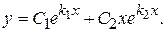
3. Корни уравнения (3) комплексно-сопряженные

Тогда, согласно определению показательной функции комплексного аргу-

мента, имеем

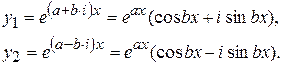
y ₁ и y ₂ - решения уравнения (2).

Рассмотрим новые функци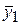и и 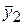, определенные равенством

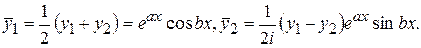
По теореме предыдущей лекци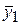и и 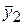- решение уравнения (2). Кроме

того,

-

- линейно независимы. Поэтому, общее решение уравнения (2) име-

ет вид

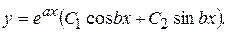
III. Уравнения со специальными правыми частями.

В общем случае частное решение неоднородного уравнения

отыскивается методом вариации произвольных постоянных. Однако, можно

указать некоторые важные для приложения частные случаи, когда част-

ное решение ищется в некотором специальном виде

1. ,

Тогда

а) если a не является корнем характеристического уравнения

(3), то частное решение ищется в виде

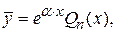
где Q_n(x) - многочлен n -ой степени с неопределенными коэффициентами

б) если a - корень характеристического уравнения кратности r,

то

r= 1,2.

2.

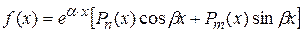
Тогда

а) если a + b×i не является корнем характеристического уравнения,

то 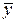ищем в виде

где Q_N(x) и G_N(x) - многочлены степени N= max{ n,m }.

б) если a + b× i является корнем характеристического уравнения, то

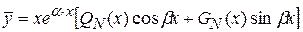
_Пример.. Найти частное решение уравнения

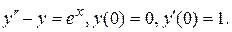
Запишем характеристическое уравнение

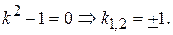
Поэтому

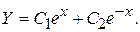
Здесь a =1, n= 0. Поскольку a является корнем характеристи-

ческого уравнения кратности 1,то частное решение неоднородного урав-

нения ищем в виде

Подставляя 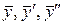в исходное уравнение, получим

Таким образом,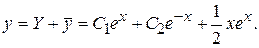

- общее решение неоднородного уравнения.

Подберем C ₁ и C ₂ так, чтобы выполнялись начальные условия:

Искомое частное решение имеет вид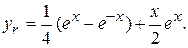

Дата добавления: 2015-05-10