Уравнение неразрывности

Элементарную струйку можно представить себе в виде пучка линий тока небольшого поперечного сечения. Сечение выбирается настолько малым, чтобы во всех его точках все параметры потока можно было считать постоянными.

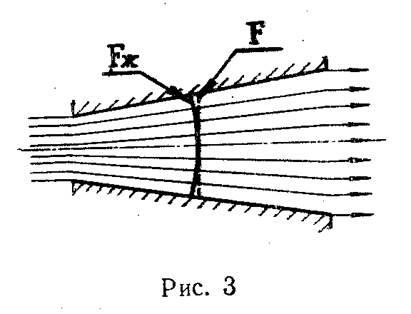
Если элементарную струйку пересечь такой поверхностью, которая будет нормальна всем линиям тока, то такое сечение называется живым сечением (рис. 3). В отличие от живого, поперечное сечение лежит в плоскости, перпендикулярной оси струйки. На рис. 3 живое сечение обозначено F_ж, а поперечное F. Нужно заметить, что понятия живого сечения и поперечного сечения применимы не только к элементарной струйке, но и к любому потоку (струе) жидкости. При небольших углах расхождения или схождения линий тока разница между живым и поперечным сечением незначительна.

Количество жидкости, проходящей через заданное сечение потока в единицу времени, представляет расход жидкости. В зависимости от того, чем именно — объемом или массой — измеряется количество жидкости, расход называют объемным или массовым и вычисляют по формулам:

(1.8)

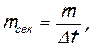(1.9)

или при неустановившемся движении:

(1.10)

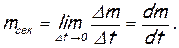(1.11)

В применявшейся ранее технической системе единиц широко использовался еще весовой расход — весовое количество жидкости, проходящей через данное сечение в единицу времени. Объемный расход измеряется в м³/сек, массовый — в кг/сек, весовой — в кГ/сек, где кГ — килограмм-сила, а кг — килограмм-масса. Объемный и массовый расходы даны в Международной системе единиц СИ, а весовой расход — в технической.

Объемный расход через живое сечение элементарной струйки равен

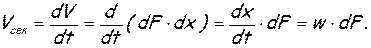
Через живое сечение потока конечных размеров объемный расход будет

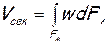(1. 12)

а если скорость по сечению постоянна, то

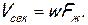(1.13)

В практических расчетах для удобства вычислений вместо живого сечения часто берут поперечное сечение и расход выражают через некоторую среднюю скорость, называемую среднерасходной скоростью. Она представляет собой такое среднее значение скорости потока в данном сечении, которое, будучи умноженным на площадь поперечного сечения, дает истинное значение объемного расхода. Следовательно,

(1.14)

Массовый расход может определяться с помощью следующей формулы:

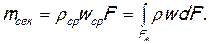(1.16)

(По аналогичной формуле вычисляется и весовой расход, только вместо массовой плотности ρ в формулу подставляется удельный вес жидкости γ.)

Произведение ρw часто используется в расчетах как самостоятельная величина, называемая плотностью тока.

Если площадка, через которую вычисляется расход, расположена под косым углом к линиям тока (или к вектору скорости), то нужно либо спроектировать площадку на направление, перпендикулярное вектору скорости, либо принимать в расчет проекцию вектора скорости на направление нормали к площадке, т.е. брать не всю скорость, а только ее нормальную составляющую 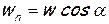[1]. Более удобен второй способ. Таким образом, в случае произвольного расположения поверхности, через которую определяется расход, относительно линий тока, расчет ведется по следующим формулам:

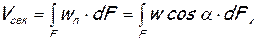(1.16)

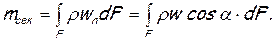(1.17)

Большое значение в газодинамике имеет уравнение неразрывности, представляющее собой гидродинамическую форму записи закона сохранения вещества. Вывод этого уравнения рассмотрим для общего случая неустановившегося движения сжимаемого газа.

Если в пространстве, через которое движется поток, выделить неподвижный объем, например, в форме параллелепипеда АВСDЕFLК. (рис.4), и определить разность массовых количеств жидкости, втекающей и вытекающей через границы объема за определенное время Δ t, то можно установить, что эта разность равна количеству жидкости, которое накапливается внутри объема за то же время. Нужно сразу заметить, что, поскольку рассматриваемый объем не меняет своих размеров и формы, накопление жидкости может происходить только за счет постепенного увеличения ее плотности[2]. Полученный вывод представляет собой закон неразрывности, или сплошности. Действительно, как это нетрудно заметить, при рассмотрении предполагается, что внутри заданного объема все заполнено жидкостью и не имеется каких-либо пустот. Подсчитаем эти количества жидкости.

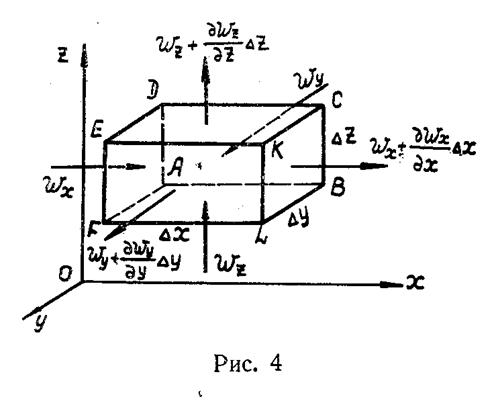
Внутрь объема АВСDЕFLК втекает:

через грань АDЕF ρ w_x Δ y Δ z Δ t,

через грань АВСD ρ w_y Δ x Δ z Δ t,

через грань АВLF ρ w_z Δ x Δ y Δ t.

Из объема АВСDЕFLК вытекает:

через грань ВСКL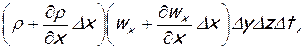

через грань ЕFLК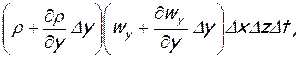

через грань СDЕК

накапливается внутри объема .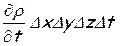

Взяв разность втекающих и вытекающих количеств и приравняв ее количеству накапливаемой жидкости, получим

Раскроем скобки, отбросим члены, содержащие малые величины второго и более высоких порядков, и приведем подобные члены. Тогда, сократив обе части равенства на ΔxΔyΔzΔt и собрав все величины в левую часть, запишем это равенство в следующем виде:

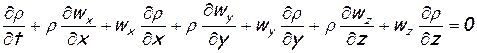(1.18)

Полученное уравнение можно записать в более компактном виде:

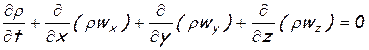(1.19)

Для сокращенного обозначения операции применяются операторы div (дивергенция) или 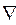(набла) заимствованные из теории поля. Тогда уравнение (1.19) запишется так:

(1.20)

Для установившегося движения ∂r/∂t = 0 и уравнение неразрывности приобретает такой вид:

div(ρw) = 0, (1.21)

а для несжимаемой жидкости, т.е. при ρ =const,

div w = 0. (1.22)

Имеется еще одна форма записи уравнения неразрывности, которая получается, если в равенстве (1.18) принять w_x = dх/dt, w_y = dу/dt, w_z = dz/dt, вынести ρ за скобку и сгруппировать члены. После небольших преобразований уравнение принимает вид

(1.23)

Если записать уравнение неразрывности для установившегося одномерного потока, для которого 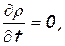w_у=0, w_z=0, то получим 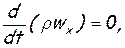следовательно

ρw_x = соnst. (1.24)

Таким образом, в одномерном установившемся потоке скорость может изменяться только за счет плотности, а в случае несжимаемой жидкости она вообще не может изменяться. Это связано с тем, что в одномерном потоке линии тока параллельны, т.е. площадь сечения потока не меняется и поперечные составляющие скорости отсутствуют.

В тех случаях, когда линии тока расходятся или сходятся под небольшим углом, поперечные составляющие скорости настолько малы, что приближенно поток можно считать одномерным, полагая, что в каждом поперечном сечении скорость имеет постоянное (среднерасходное) значение и изменяется только по длине потока. При таком рассмотрении потока удобно пользоваться уравнением неразрывности в такой форме, которая получается из условия равенства массовых расходов на входе и выходе расчетного участка, а именно:

m_сек1 = m _сек2,

или

ρ₁ w₁F₁ = ρ₂w₂F₂, (1.25)

Для несжимаемой жидкости ρ=const и, следовательно.

w₁F₁ = w₂F₂, (1.26)

т.е. объемные расходы равны на входе и выходе. В этих формулах под ρ и w подразумеваются их среднерасходные значения, а под F — площади поперечного сечения.

Уравнения неразрывности в форме (1.25) и (1.26) широко применяются в практических расчетах.

[1] Здесь α — угол между вектором скорости и нормалью к площадке.

[2] Так, например, для несжимаемой жидкости (ρ=соnst) накопления быть не может, поэтому разность количеств втекающей и вытекающей жидкости равна нулю.

Дата добавления: 2015-05-10