Погрешности прямых измерений

Положим, что систематические погрешности исключены и погрешности результатов измерений являются только случайными. Обозначим буквами - результаты измерений физической величины, истинное значение которого равно . Абсолютные погрешности результатов отдельных измерений обозначены:

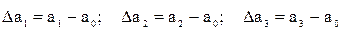(1)

Суммируя получено левые и правые стороны равенства (1), получим:

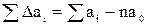(2)

В основе теории случайных погрешностей лежат подтверждаемые опытом предположения:

- погрешности могут принимать непрерывный ряд значений;

- при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

- вероятность появления погрешности уменьшается с ростом ее величины. Необходимо также, чтобы погрешности были малы по сравнению с измеряемой величиной и независимы.

Согласно предположению (1) при числе измерений n ® ¥ получим

,

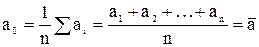Однако, всегда число измерений конечно и остается неизвестным. Но для практических целей достаточно найти экспериментальным путем значение физической величины настолько приближающееся к истинному, что может быть использована вместо истинного. Вопрос в том, как оценить степень этого приближения?

По теории вероятности среднее арифметическое серии измерений достовернее результатов отдельных измерений, т.к. случайные отклонения от истинного значения в разные стороны равновероятны. За вероятность a появления величины a_i в интервале шириной 2Da_i понимают относительную частоту появления значений a_i, попадающих в интервал 2Da_i к числу всех появляющихся значений a_i при числе опытов (измерений), стремящихся к бесконечности. Очевидно, что вероятность достоверного события равна единице, вероятность невозможного события равна нулю, т.е. 0 £ a £ 100 %.

Вероятность того, что искомая величина (истинное значение ее) содержится в интервале (a - Da, a + Da) назовем доверительной вероятностью (надежностью) a, а соответствующий a интервал (a - Da, a + Da) - доверительным интервалом; чем меньше величина погрешности Da, тем меньше и вероятность того, что измеряемая величина содержится в интервале, определенной этой погрешностью. Верно и обратное утверждение: чем меньше надежность результата, тем уже доверительный интервал искомой величины.

При большом n (практически при n ³ 100) полуширина доверительного интервала при заданной надежности a равна

, (3)

где K(a) = 1 при a = 0,68; K(a) = 2 при a = 0,95; K(a) = 3 при a = 0,997.

При малом числе измерений, что чаще всего и встречается в студенческом лабораторном практикуме, коэффициент K(a)в (3) зависит не только от a, но еще и от числа измерений n. Поэтому мы всегда будем при наличии только случайной погрешности полуширину доверительного интервала находить по формуле

(4)

В (4) коэффициент t_an называется коэффициентом Стьюдента. Для a = 0,95 принятой в студенческом практикуме, значения t_an таковы:

n
tan		4,3	3,2	2,8	2,6	2,5	2,4	2,3	2,3

Величину называют среднеквадратичной погрешностью среднего арифметического из серии измерений.

Погрешность прибора или меры обычно указывается в паспорте его (ее) или условным знаком на шкале прибора. Обычно под погрешностью прибора d понимают полуширину интервала, внутри которого с вероятностью измерений 0,997 может быть заключена измеряемая величина, если погрешность измерений обусловлена только погрешностью прибора. В качестве общей (полной) погрешности результата измерений примем с вероятностью a = 0,9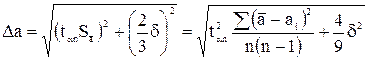5

, (5)

Абсолютная погрешность позволяет установить в каком знаке полученного результата содержится неточность. Относительная погрешность дает информацию о том, какую долю (процент) измеряемой величины составляет погрешность (полуширина доверительного интервала).

Окончательный результат серии прямых измерений величины a₀ запишем в виде

.

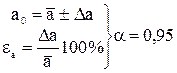Например

(6)

Таким образом, любая физическая величина, найденная опытным путем, должна быть представлена:

- средним значением ;

- доверительной величиной a;

- полушириной доверительного интервала Da.

Дата добавления: 2015-05-10