Явления переноса и вязкость

Молекулярный механизм переноса.

Перенос количества движения, тепла и массы.

Общее свойство всех трех видов переноса

Вязкость, теплопроводность и диффузия.

Закон Ньютона о молекулярном трении в жидкости.

Слоистое течение. Динамический коэффициент вязкости.

«Равновесные состояния вещества характеризуются равномерным распределением в пространстве всех его параметров, причем каждый элемент вещества находится в механическом и тепловом равновесии с соседними элементами. Если некоторые параметры вещества в исходном состоянии распределены неравномерно, то между соседними элементами вещества происходит механический или тепловой обмен, который всегда приводит вещество в равновесное состояние, т.е. стремится сгладить имеющиеся в нем неоднородности. Существование этого стремления к равновесию в неоднородном веществе, которое в классической термодинамике принимается без доказательства, по-видимому, требует только, чтобы смежные части вещества взаимодействовали определенным образом. Характер этого взаимодействия может зависеть от молекулярного строения смежных частей вещества и от физических свойств процессов переноса, зависящих от конкретного параметра, который распределен неравномерно, однако тенденция к равновесию между взаимодействующими частями вещества имеет вполне общий характер и не зависит, как и все результаты классической термодинамики, от конкретного строения данного вещества.

Важный и общий результат обмена между двумя элементами вещества с различными параметрами состоит в том, что величина некоторого количества, удовлетворяющего закону сохранения, связанная с одним элементом, уменьшается, а величина, связанная с другим элементом, увеличивается. В целом ряд таких обменов составляет то, что называют явлением переноса. Три основных вида этого явления – это переносы вещества (массы), энергии и количества движения. Основное внимание … обращено на общие свойства этих трех видов переноса. Мы не будем привлекать конкретные молекулярные свойства вещества, хотя иногда на них придется ссылаться для удобства и выяснения природы молекулярного механизма переноса в жидкостях».

& (Бэтчелор) с. 50 …51

«Процессы молекулярного переноса в газах (и жидкостях) – вязкость (внутреннее трение), теплопроводность и диффузия – имеют большое значение для правильного объяснения целого ряда физических и физико-химических явлений, а также для решения многих технологических и конструктивных задач, связанных с переносом массы, количества движения и тепла.

…Исследование вязкости газов и газовых смесей и зависимости ее от температуры и давления необходимо, прежде всего, как изучение одной из основных констант, характеризующих физические свойства веществ.

Коэффициент вязкости является наиболее изученной величиной процессов молекулярного переноса. Он в известной мере определяет также коэффициенты диффузии и теплопроводности для газообразного состояния, так как последние можно приближенно вычислять из коэффициентов вязкости на основе уравнений молекулярно-кинетической теории.

…Насущная необходимость в сведениях по вязкости газов и газовых смесей для решения ряда конструктивных и технологических задач как в промышленной практике (для расчетов многочисленных процессов, протекающих при атмосферном и при высоких давлениях), так и в разработке новых технологических процессов и аппаратов, определяется, прежде всего, тем, что в формулы расчета гидравлического сопротивления и теплообмена коэффициент вязкости входит как один из основных параметров».

& (Голубев) с. 5 …6

Голубев Илья Федорович – автор монографии «Вязкость газов и газовых смесей» (1959) и один из авторов справочника азотчика (МХП, ГИАП 1947).

«В жидкой смеси, состав которой изменяется в зависимости от координат, возникает перенос особого вида§. Предположим, что молекулы одной составной части смеси отмечены определенным образом. Все молекулы находятся в непрерывном хаотическом движении и вследствие этого имеют тенденцию к удалению от какого-либо начального положения. В таком случае если в некоторый момент времени количество отмеченных молекул вблизи одной стороны элемента поверхности, проведенной в жидкости, больше чем на другой, то случайное блуждание … молекул в обоих направлениях через элемент поверхности приводит в общем случае к ненулевому потоку ( отмеченных – В.Г.) молекул через него; направление этого потока таково, что он приводит к выравниванию количества отмеченных молекул с обеих сторон поверхности¨. Этот ненулевой поток одной из частей жидкой смеси, создаваемый перемещением самих молекул, порождает диффузию вещества (массодиффузию)…

Перенос кинетической энергии молекулярного движения осуществляется путем взаимодействия соседних молекул (или в результате столь малых расстояний между молекулами, что одна находится в пределах действия поля сил другой, как в случае твердых тел и жидкостей, или в результате случайных столкновений, как в случае газа). Условия, при которых происходит перенос только энергии молекул, т.е. тепловой энергии, известны из эксперимента. Две массы жидкости, разделенные тонкой жесткой стенкой, проницаемой для тепла, находятся в тепловом равновесии, если функция состояния, называемая температурой, имеет одинаковые значения для этих масс; а если две температуры не равны, то существует некоторый ненулевой поток тепла через границу в направлении убывания температуры. Удаление стенки, разделяющей эти две массы при одном и том же давлении, очевидно, не влияет на условие теплового равновесия или на направление указанного теплового потока в том случае, когда две температуры различны, хотя величина теплового потока изменяется ввиду того, что давления при отсутствии стенки должны оставаться одинаковыми. Этот поток энергии молекул, когда температура распределена неравномерно, создает теплопроводность.

Перенос количества движения молекул через элемент поверхности, движущейся с локальной макроскопической скоростью жидкости, возникает в том случае, когда молекулы пересекают поверхность (так будет в газе – В.Г.), и он всегда происходит, если имеется сила взаимодействия между двумя группами молекул на обеих сторонах элемента поверхности (так происходит в жидкости – В.Г.). Суммарный эффект потока количества движения при прохождении молекул через элемент поверхности и сил, создаваемых между молекулами на его обеих сторонах, представляется в виде локального напряжения в жидкости. Напряжение в какой-либо точке жидкости есть результат движения молекул и их взаимодействий в окрестности этой точки, поэтому если скорость жидкости постоянна в этой окрестности, то напряжение имеет вид, соответствующий покоящейся жидкости, и направлено по нормали к элементу поверхности при любой его ориентации. Если же скорость жидкости непостоянна в этой окрестности, то касательные напряжения могут быть отличными от нуля.

Закон изменения векторной функции координат, например скорости жидкости, в окрестности какой-либо точки не очевиден и будет рассмотрен в гл. 2 (Гл. 2. Кинематика поля течения – В.Г.); напряжение, связанное с этим изменением скорости, будет полностью описано в гл. 3 (Гл. 3. Уравнения движения жидкости – В.Г.). Однако пока можно использовать понятие переноса количества движения в рамках предварительного обсуждения, ограничиваясь частным случаем (имеющим, однако, как будет установлено позже, фундаментальное значение), когда скорость жидкости по отношению к элементу поверхности (движущемуся вместе с жидкостью) расположена в его плоскости и имеет величину, которая изменяется только по нормали к этому элементу поверхности; такое движение называется простым сдвигом, при котором плоскости жидкости, параллельные элементу поверхности, скользят как жесткие друг над другом. В этих условиях очевидно, что если скорости жидкости по обе стороны элемента поверхности различны, то любое случайное взаимодействие молекул через этот элемент приводит к появлению касательной составляющей напряжения, а знак напряжения будет таким, который соответствует уменьшению разности скоростей по обе стороны от элемента поверхности. Перенос количества движения создает таким образом внутреннее трение, а жидкость, в которой проявляется внутреннее трение, называется вязкой.

Основные общие свойства всех трех видов переноса состоят в следующем: во-первых, результирующий поток некоторой величины (числа отмеченных молекул, тепла, количества движения) равен нулю тогда, когда связанная с ней другая величина, характеризующая локальную интенсивность (долю отмеченных молекул, температуру, скорость жидкости), распределена равномерно в пространстве; во-вторых, направление движения ненулевого результирующего потока через элемент поверхности в веществе таково, что происходит выравнивание интенсивности по обе его стороны».

& (Бэтчелор) с. 51 …53

«Ньютон [ Ньютон И. Математические начала натуральной философии (1686). См. Собрание трудов, т. VII. Изд. АН СССР, 1936] впервые высказал в виде гипотезы закон для внутреннего трения:

«Сопротивление, возникшее вследствие недостатка скольжения между частицами жидкости, при прочих равных условиях пропорционально скорости, с которой частицы отклоняются одна от другой».

На основе этой гипотезы Ньютон сформулировал следующий постулат:

«Если твердый, бесконечно длинный цилиндр вращается около оси с постоянной угловой скоростью в бесконечной жидкой среде и если последняя приобретает вращательное движение исключительно за счет импульса, сообщаемого цилиндром, то я утверждаю, что периоды вращения частиц жидкости пропорциональны их расстояниям от оси цилиндра».

Обстоятельная интерпретация и четкая (словесная) формулировка закона внутреннего трения были даны значительно позднее Н.П. Петровым [ Петров Н.П.. Трение в машинах и влияние на него смазывающей жидкости. Инженерный журнал, 1883].

Петров Н.П. – основоположник гидродинамической теории смазки машин.

Этот закон гласит, что между двумя соседними слоями в направлении, противоположном движению, действует сила (отнесенная к единице поверхности соприкосновения слоев), пропорциональная изменению скорости в направлении, перпендикулярном к движению:

, (1)

где ∆w - изменение скорости в двух соседних слоях, находящихся на расстоянии ∆y.

Более точно в дифференциальной форме эта формула имеет вид

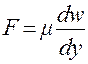, (1а)

Коэффициент пропорциональности m называется коэффициентом внутреннего трения или коэффициентом динамической вязкости; в дальнейшем будем называть его просто коэффициентом вязкости».

& (Голубев) с. 7 … 8

«Наличие силы сопротивления при сдвиге можно обнаружить опытом (что и сделал в свое время Ньютон – В.Г.), схема которого приведена на рисунке 4. На неподвижной нижней пластинке – слой жидкости толщиной y₀, на свободной поверхности – легкая пластинка площадью S. Если к пластине приложить силу R, пластинка начнет перемещаться. После некоторого «разгонного» интервала времени установится равномерное движение пластинки с некоторой скоростью w₀. Это означает, что за время разгона возникает приложенная к пластинку сила сопротивления R _τ= – R. Эта сила может быть только силой сопротивления жидкости (сопротивление воздуха мало и во внимание не прини­ма­ется).

Механизм возникновения силы сопротивления можно представить следующим образом. Слой жидкости, прилегающий к пластинке, прилипает к ней и движется вместе с пластинкой со скоростью w₀. Вследствие молекулярных связей этот слой увлекает за собой следующий и т.д. Поскольку нижний слой примыкает к неподвижной пластинке, его скорость равна нулю. Таким образом, в жидкости возникает слоистое движение с некоторым распределением скоростей по высоте w=ƒ(y).

В рассматриваемом случае распределение скоростей линейное. Вследствие действия межмолекулярных связей между движущимися слоями жидкости возникают силы вязкости или внутреннего трения. Ньютон указал на те параметры, от которых зависит величина этой силы R_τ. Для рассматриваемого слоистого движения

,

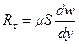где μ – динамический коэффициент вязкости; S – площадь соприкосновения слоев; - градиент скорости, являющийся показателем интенсивности изменения величины скорости по нормали к ее направлению.

Можно показать, что градиент скорости при слоистом движении жидкости равен скорости сдвиговой деформации».

& (Емцев) с. 17…18

«Опыт показывает, что… скорость между пластинами распределена линейно:

w= w₀ y/y₀, давление постоянно во всей области. Такое течение называют течением чистого сдвига. … Измерения показыв ают, что напряжения трения 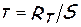пропорционально отношению скоростиw₀ к расстоянию между пластинами y₀ и не зависит от абсолютной величины скорости (имеет значение лишь относительное движение слоев жидкости). Отношение w₀ /y₀ = dw/dy называется градиентом скорости по нормали к плоскости скольжения слоев или кратко – поперечным градиентом скорости

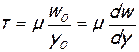(1.11)

Формула (1.11) выражает закон Ньютона о молекулярном трении в жидкости – напряжение трения пропорционально поперечному градиенту скорости. Этот закон был установлен Ньютоном экспериментальным путем. Жидкости, удовлетворяющие уравнению (1.11), называются ньютоновскими.

… Коэффициент пропорциональности , [ Н∙с/м² ] называется динамическим коэффициентом вязкости или просто вязкостью жидкости. Величина μ зависит от природы жидкости, ее агрегатного состояния, температуры и практически не зависит от давления в широком диапазоне его изменения. Чем больше μ, тем больше вязкость жидкости».

& (Сергель) с. 15

Вопрос! Каков физический смысл μ?

«Из уравнения (1) следует, что величина m равна той силе, которую испытывает единица поверхности одного из слоев со стороны другого слоя, если изменение (градиент) скорости между ними равно единице.

В системе CGS (СГС) единица вязкости определяется как вязкость вещества, в котором при градиенте скорости 1 см/с на 1 см на каждый квадратный сантиметр действует сила трения, равная одной дине. Эта единица вязкости называется пуаз и обозначается буквой П, ее сотая часть называется сантипуаз (СП).

(В системе СИ размерность вязкости - Н∙с/м²)

… Величина, обратная вязкости, называется текучестью и обозначается через φ:

φ=1/μ.

& (Голубев) с. 8

«Вязкость газов непосредственно связана с другими процессами молекулярного переноса – диффузией и теплопроводностью. Эти три явления представляют близкую аналогию, все они связаны с переносом какой либо величины (вязкость – количества движения, диффузия – массы и теплопроводность – тепловой энергии), причем перенос ее из одной части газа в другую происходит до тех пор, пока данная величина не распределится равномерно по всему объему. Эти процессы необратимы; они ведут к выравниванию плотностей, температур и скоростей, к достижению равновесного состояния, отвечающего минимуму свободной энергии или максимуму энтропии. С точки зрения кинетической теории механизм всех трех процессов весьма схож, также схожи и уравнения, определяющие их.

Если для вязкости простой молекулярно-кинетический вывод приводит к уравнению

,

то для диффузии аналогичный вывод дает:

,

и для теплопроводности

.

Более строгие выводы приводят лишь к замене 1/3 другой численной постоянной.

Соотношения, связывающие коэффициенты m, D и λ, имеют вид

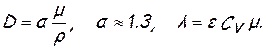
Коэффициент e приблизительно равен 2,5 для одноатомных газов, 1,9 для двухатомных и 1,75 – 1,5 для трех- и многоатомных. Экспериментальные данные показывают, однако, что e является некоторой функцией температуры. Хорошее согласование с опытом дает следующее уравнение [ Тимирязев А.К. Кинетическая теория материи. ГТТИ, 1933.]:

, где .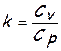

Экспериментальные данные по вязкости и теплопроводности газов при высоких давлениях показывают, что e есть функция также и давления». & (Голубев) с. 24 … 25

§ Такой перенос наблюдается также и в твердом теле, например, в сплаве, состоящем из молекул разных видов, поскольку молекулы в твер­дом теле не сохраняют абсолютно одно и то же положение в решетке, хотя скорость переноса в твердом теле намного меньше, чем в жидкости.

¨ Можно было бы предположить, что условием ненулевого потока отмеченных молекул через элемент поверх­ности является различие их числовой плотности (числа в единице объема) по обеим сторонам поверхности. Когда плотность жидкости постоянна, выбор между этими двумя условиями ненулевого потока не имеет различия. Но если плотность жидкости не постоянна (что, как правило, влечет за собой также и непостоянство температур), то стремление отмеченных молекул двигаться - путем хаотического движения – по отношению к неотмечен­ным молекулам проявляется в основном в результате неодинакового относительного количества отмеченных и неотмеченных молекул по обеим сторонам поверхности, а не вследствие неодинаковой их числовой плотности.

Дата добавления: 2015-05-10