Решение систем уравнений

Круг

Время	1 тур (05.10.13)	2тур (12.10.13)	3тур (19.10.13)	4 тур (26.10.13)	5тур (02.11.13)
9.00	Приват-2 - Евраз	Штурм - Взрывпром	Гетьман - ЦС Олимп	ЦС Олимп - Дзержинка	Гетьман - Союз
9.45	ЦС Олимп - Взрывпром	Приват-2 - ЦС Олимп	Штурм - Эгида	Штурм - Евраз	Эгида - ЦС Олимп
10.30	Эгида - Дзержинка	Евраз - Заречный	Юпитер - Дзержинка	Гетьман - Юпитер	Евраз - Юпитер
11.15	Союз - Юпитер	Юпитер - Эгида	Союз - Взрывпром	Эгида - Карат	Приват-2 - Штурм
12.00	Штурм - Гетьман	Гетьман - Карат	Евраз - Карат	Приват-2 - Союз	Взрывпром - Карат
12.45	Карат - Заречный	Союз - Дзержинка	Приват-2 - Заречный	Взрывпром - Заречный	Дзержинка - Заречный

MathCAD предлагает средства для решения системы уравнений. Максимально возможное количество уравнений и переменных в системе равно 50. Результатом решения системы является числовое значение искомых корней. Для решения уравнений и систем уравнений в MathCad существует несколько средств. Рассмотрим одно из них с использованием ключевых полей Given и find.

Для решения системы уравнений, с помощью функции find() необходимо выполнить

- задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов;

- напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений;

- ввести уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, £ и ³;

- ввести любое выражение, которое включает функцию Find, например: а:= Find (х, у).

Пример 2.3

Решить систему уравнений с помощью блока Given – find():

.

Указания

На рис. 2.4 приведен фрагмент решения системы уравнений в MathCad.

Рис. 2.4. Фрагмент рабочего листа с решением системы уравнения
с помощью матричных функций

С помощью ключевых слов Given и Find можно выполнять решение уравнений и систем уравнений линейного и нелинейного вида.

MathCad позволяет решать уравнения и в матричном виде. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х ₁, х ₂, …, х_n:

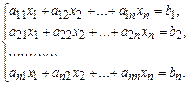
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде АX = B, где:

Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы.

Матрица-столбец B, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы.

Матрица-столбец X, элементы которой – искомые неизвестные, называется решением системы.

Если определитель матрицы A неравен нулю, то рассматриваемая система, или эквивалентное ей матричное уравнение, имеет единственное решение:

AX=B

A^-1AX= A^-1B

X= A^-1B

Системы линейных уравнений удобно решать с помощью функции lsolve.

lsolve(А, B) – возвращается вектор решения X такой, что АX = B, где

А – квадратная, не сингулярная матрица.

B – вектор, имеющий столько же рядов, сколько рядов в матрице А.

Пример 2.4

Решить систему уравнений примера 12.3 матричным способом.

Указания

На рис. 2.5 показано решение системы двух линейных уравнений относительно двух неизвестных (двумя способами).

Рис.2.5. Фрагмент рабочего листа с решением системы уравнений
с помощью функции find()

Пример 2.5

Выполнить решение системы линейный уравнений примера 2.3 методом Крамера.

Указание

1. Для решения системы уравнений методом Крамера необходимо построить две дополнительные матрицы для вычисления определителей. Эти матрицу могут быть сформированы с помощью специальных функций выделения и замены части матрицы.

2. Пример использования таких функций приведен на рис. 2.6.

Рис. 2.6. Фрагмент рабочего листа с решением системы
линейных уравнений методом Крамера

ИНДИВИДУАЛЬНАЯ РАБОТА

«Решение систем линейных алгебраических уравнений».

Задание: Решить СЛАУ с помощью встроенной функции lsolve(M,V) и с помощью блока GIVEN…Find(x1,x2,x3). Результаты сравнить.

Вариант№1

Вариант №2

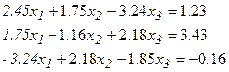
Вариант №3

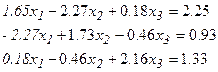
Вариант №4

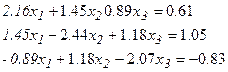
Вариант №5

Вариант №6

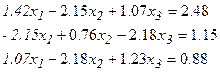
Вариант №7

Вариант №8

Вариант №9

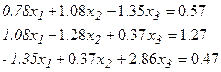
Вариант №10

Вариант №11

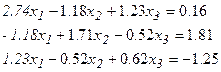
Вариант №12

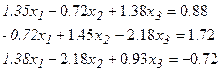
Контрольные вопросы

1. Какие средства MathCad можно применять для решения уравнений и систем уравнений?

2. Какие из этих средств можно применять для решения систем уравнений?

3. Как установить знак логического равенства?

4. В каких случаях MathCAD не может найти корень уравнения?

5. Опишите структуру блока решения уравнений.

6. Опишите способы использования функции Find.

7. В каких случаях MathCAD не может найти решение системы уравнений?

8. Какие уравнения называются матричными?

Дата добавления: 2015-05-10