Определение динамических коэффициентов

Из линеаризованной системы уравнений продольного движения найдем динамические коэффициенты по соответствующим формулам

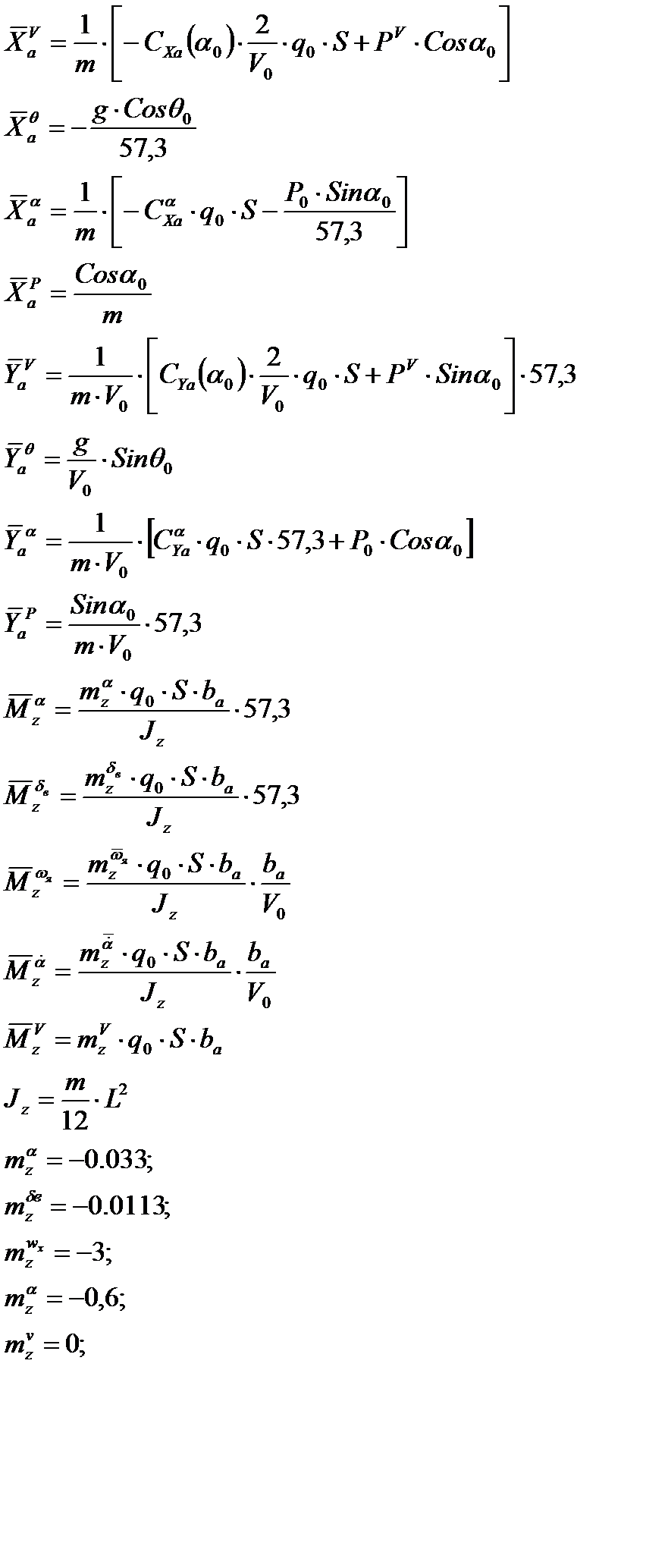
где V₀, a₀, R₀ – невозмущенные значения переменных.

H=5500М

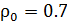
g=9.79

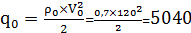
Найдем, что скорости V₀ соответствует тяга Р₀ = 21017 Н, a₀ = 5. По графику зависимости С_Ха(a) найдем, что С_Ха(a₀) = 0,0211, соответственно С_Ya(a₀) = 0,41. По формулам и 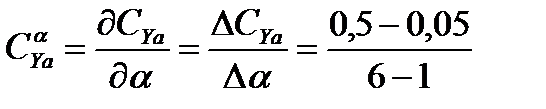получим значения 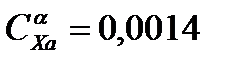и .

Подставляя все известные нам данные в перечисленные выше формулы, получим численное значение динамических коэффициентов.

На основе системы линеаризованных уравнений продольного движения можно получить передаточные функции и проанализировать устойчивость с помощью характеристического уравнения

Данное уравнение приводится к виду:

Практические расчеты переходных процессов и корней характеристического уравнения показывают, что для статически устойчивого по углу атаки ЛА наблюдается быстрое движение, соответствующее балансировки моментов и большим по модулю корнями заканчивающееся в течение нескольких секунд, и медленное движение, соответствующее балансировке сил и малым по модулю корнями продолжающееся до тех пор, пока на наступит равновесие сил, действующих на самолет.

Из сказанного следует, что короткопериодическая и длиннопериодическая составляющие продольного движения самолета как бы разнесены во времени. Это дает возможность рассматривать их раздельно.

Однако отдельно рассматривать длиннопериодическое движение можно только в том случае, когда установлено, что короткопериодическое движение затухающее.

Быстрое (угловое) движение происходит по угловой скорости w_z и углу атаки a, медленное (траекторное движение) – по скорости V и углу наклона траектории q.

Быстрое движение называют короткопериодическим. Для статически устойчивого ЛА ему соответствуют обычно комплексно-сопряженные корни характеристического уравнения, которые приближенно можно получить из усеченного уравнения

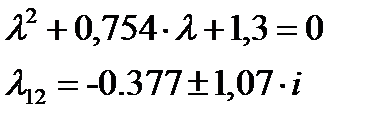
Мы получили комплексно-сопряженные корни, значит можно сделать вывод, что короткопериодическое движение будет колебательным.

Найдем декремент затухания, частоту и период короткопериодического движения. Т.к. данное уравнение можно представить в виде колебательного звена, то декремент затухания x, частоту w и период Т найдутся из системы

Медленное движение называется длиннопериодическим или фугоидным. Ему часто соответствуют тоже комплексно-сопряженные корни, которые приближенно можно получить из усеченного уравнения

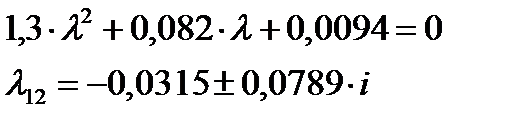
Мы получили комплексно-сопряженные корни, значит можно сделать вывод, что длиннопериодическое движение будет колебательным.

Найдем декремент затухания, частоту и период длиннопериодического движения. Т.к. данное уравнение можно представить в виде колебательного звена, то декремент затухания x, частоту w и период Т найдутся из системы

Сравнивая периоды при короткопериодическом и длиннопериодическом движении получаем, что Т при КПД < T при ДПД. Следовательно, отсюда можно сделать вывод, что быстрое движение действительно является короткопериодическим, а медленное движение – длиннопериодическим.

Выводы

В данной работе мы рассмотрели аэродинамику самолета и его поведение на отклонение рулевых органов. По полученным данным можно сказать, что самолет является статически устойчивым, т.к. наклон кривой зависимости δбал(αбал) является отрицательным.

Как правило, полеты происходят на углах атаки, меньших критических. В нашем случае, полет будет происходит при углах атаки меньше αкр=19°.

Корни усеченного уравнения соответствующего короткопериодическому движению и длиннопериодическому движению различаются с корнями характеристического многочлена на малую величину в связи с произведенными округлениями.

Дата добавления: 2015-05-10