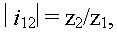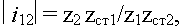Планетарные передачи

Планетарные механизмы появились на американских автомобилях в начале этого столетия. Их использование на легковых автомобилях и грузовиках малой грузоподъемности было обусловлено неоспоримым преимуществом: минимальные габариты по сравнению с обычными зубчатыми передачами. Вальные коробки передач со скользящими зубчатыми колесами на ранних этапах развития не имели синхронизаторов, и это требовало особой квалификации при переключении передач. Первые планетарные коробки передач имели только две передачи, хотя имеется информация о том, что в 1906 году Кадиллак использовал планетарный механизм, реализующий три передачи. Ранние конструкции планетарных коробок передач имели ряд существенных недостатков. Они были шумные, имели малую долговечность подшипников (в то время для устанавливки шестерен на валы использовались подшипники скольжения) и из-за перекосов вызванных их неравномерным износом вибрировали при включении ленточных тормозов. Появление вальных коробок передач с передвижными каретками приводит, в конечном счете, к их большей популярности по сравнению с планетарным коробками, и, практически, к повсеместному их использованию на легковых автомобилях и грузовиках. Однако, на автомобиле Форд-T, планетарная коробка использовалась вплоть до 1928 года. Планетарные передачи были вновь использованы в 1930 году Bоrg-Warner в автоматической коробке передач "Дженерал Моторс" Hydra-Matic. Проведенный большой объем исследований, а также использование косозубых зацеплений, легированных сталей, термообработки металла и игольчатых подшипников устранили многие недостатки ранних конструкций планетарных передач. Планетарные передачи сегодня имеют широчайший диапазон использования в легковых автомобилях, грузовиках и гусеничной технике. ОСНОВНЫЕ ПОНЯТИЯ Определим общие понятия, используемые при рассмотрении зубчатых передач. Передаточное отношение механизма. Это отношение частоты вращения ведущего вала к частоте вращения ведомого вала. Понижающая передача. Передача, передаточное отношение которой по абсолютной величине больше 1. В этом случае крутящий момент на ведомом валу механизма больше момента на ведущем валу на величину передаточного отношения, а частота вращения ведомого вала на эту же величину меньше частоты вращения ведущего вала. Повышающая передача. Передача, передаточное отношение которой по абсолютной величине меньше 1. В этом случае крутящий момент на ведомом валу механизма меньше момента на ведущем валу на величину передаточного отношения, а частота вращения ведомого вала на эту же величину больше частоты вращения ведущего вала. Прямая передача. Передача, передаточное отношение которой равно 1, т.е. крутящий момент и частота вращения ведомого вала остаются равны частоте вращения и моменту ведущего вала. УСТРОСТВО И СВОЙСТВА ПЛАНЕТАРНОГО РЯДА (МЕХАНИЗМА) Конструкции планетарных рядов достаточно разнообразны. Познакомимся с устройством планетарного ряда на примере наиболее простого и часто используемого (рис.1). Он состоит из малого центрального колеса (солнца), которое находится в постоянном зацеплении с шестернями, называемыми сателлитами. Сателлиты могут вращаться относительно осей, установленных в водиле. Зубчатое колесо внутреннего зацепления, называемое большим центральным колесом (эпициклом, короной), находится в постоянном зацеплении с сателлитами и окружает всю конструкцию. Следует отметить, что малое центральное колесо, водило и большое центральное колесо вращаются относительно одной общей оси, в то время, как сателлиты планетарной передачи вращаются относительно собственных осей и вместе с водилом относительно общей оси. При этом следует отметить, что сателлиты планетарной передачи являются составной частью водила.

Рис.1.	1 - малое центральное колесо;	3 - водило;
	2 - большое центральное колесо;	4 - сателлиты

Название этого механизма происходит от сателлитов, которые подобно планетам, вращаются относительно своих осей и в то же время вокруг малого центрального колеса (солнца).

Что же так привлекает конструкторов к планетарным механизмам? Здесь можно перечислить несколько пунктов:

1. Все элементы планетарной передачи вращаются относительно общей оси, что делает ее компактной.

2. Планетарные передачи, не смотря на их компактные размеры, могут передавать большие крутящие моменты по сравнению к другим типами передачи. Это объясняется тем, что момент передается несколькими сателлитами планетарной передачи, что позволяет значительно снизить контактные напряжения на поверхностях зубьев при передаче момента.

3. Расположение элементов планетарного ряда позволяет относительно легко организовывать их систему управления (имеется в виду оборудование тормозами и блокировочными муфтами).

4. При удачном выборе кинематической схемы КПД таких передач имеет высокое значение

Основным параметром, определяющим свойства планетарного ряда, является внутреннее передаточное отношение. В общем случае любой планетарный ряд характеризуется шестью внутренними передаточными отношениями. Однако, на практике обычно используется только одно, определяемое как отношение частоты вращения малого центрального к частоте вращения большого центрального колеса при остановленном водиле:

где	1 - индекс малого центрального колеса;
	2 - индекс большого центрального колеса;
	3 - индекс водила.

В зависимости от того, как вращаются центральные колеса при остановленном водиле, внутреннее передаточное отношение планетарного ряда может быть либо положительным, либо отрицательным. Если они вращаются в одном и том же направлении, то внутреннее передаточное отношение положительное, в противном случае оно отрицательное. Так для простого планетарного ряда, представленного на рис.1, центральные колеса при остановке водила будут вращаться в различных направлениях, и, следовательно, внутреннее передаточное отношение этого ряда - отрицательное.

Все планетарные ряды в зависимости от знака внутреннего передаточного отношения, определенного при остановленном водиле, классифицируются на два класса:

1. Планетарные ряды с положительным внутренним передаточным отношением.

2. Планетарные ряды с отрицательным внутренним передаточным отношением.

Как уже отмечалось, кинематических схем построения планетарных рядов имеется достаточно большое количество. Наиболее известным планетарным рядом для всех автолюбителей является дифференциал (рис.2), без которого не обходится не один современный автомобиль. Наверное, не многие догадываются, что дифференциал есть не что иное, как планетарный ряд.

Рис2.	1 - центральное колесо;	3 - сателлиты
	2 - водило;

Отличительной особенностью дифференциала является то, что он имеет центральные колеса одинакового размера, поэтому внутреннее передаточное отношение этого механизма равно -1. Минус, очевидно, означает, что дифференциал относится ко второму классу планетарных механизмов, т.е. при остановленном водиле центральные колеса вращаются в разные стороны.

Рассмотрим другие типы планетарных рядов. На рисунке 3 представлены планетарные ряды, относящиеся к первому классу.

Рис.3	1 - малое центральное колесо;	4 - одновенцовые сателлиты;
	2 - большое центральное колесо;	5 - двухвенцовые сателлиты.
	3 - водило;

Примеры построения планетарных рядов, относящихся ко второму классу, представлены на рисунке 4.

Рис.4	1 - малое центральное колесо;	4 - сателлиты;
	2 - большое центральное колесо;	5 - двухвенцовые сателлиты.
	3 - водило;

Планетарные ряды, изображенные на рисунках 3а, 3в, 4б, 4в, построены с использованием двухвенцовых сателлитов. Планетарный ряд, построенный по схеме 4в, носит название несимметричного дифференциала, а ряд, представленный на рисунке 4г называется планетарным рядом со сцепленными сателлитами.

Как видно из приведенных примеров, планетарный ряд можно построить, используя только внутреннее зацепление (рис.3а), только внешнее зацепление (рис.3в и 4г), только конические передачи (рис.2 и 3в) или с использованием внутреннего и внешнего зацеплений (рис.3б, 4а, 4б).

Уравнение, связывающее угловые скорости () трех основных звеньев любого планетарного ряда (не зависимо от схемы построения) выглядит следующим образом:

где	1 - индекс малого центрального колеса;
	2 - индекс большого центрального колеса;
	3 - индекс водила.

Вы спросите: "А как, все-таки, определить величину внутреннего передаточного отношения планетарного ряда i ₁₂?". Нет ничего проще. Модуль этой величины можно легко определить, зная число зубьев шестерен, входящих в состав планетарного ряда. Для планетарных рядов с одновенцовыми и сцепленными сателлитами

где	z₁ - число зубьев малого центрального колеса;
	z₂ - число зубьев большого центрального колеса.

Для планетарных рядов с двухвенцовыми сателлитами эта величина может быть определена следующим образом:

где	z_ст1 - число зубьев сателлита, сцепленного с малым центральным колесом;
	z_ст2 - число зубьев сателлита, сцепленного с большим центральным колесом.

Таким образом, зная величину внутреннего передаточного отношения, а для конкретного планетарного ряда она постоянна, и имея зависимость, связывающую угловые скорости трех основных звеньев планетарного ряда, можно определить свойства этого механизма.