
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойство работать в редукторном режиме
|
|
|
|
Свойство блокировки планетарного ряда.
Нетрудно показать, что если угловые скорости двух звеньев планетарного ряда равны, то и угловая скорость третьего звена будет равна угловой скорости этих двух звеньев. Пусть, например,  1=
1= 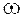 3, тогда
3, тогда
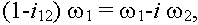
или
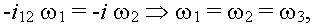
т.е. угловые скорости всех звеньев в этом случае равны, и планетарный ряд будет вращаться как одно целое тело. Аналогичный результат можно получить и в двух других случаях, когда  1=
1= 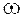 2 и
2 и  2=
2= 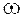 3. Отсюда вытекает известное свойство блокировки планетарного ряда: если установить блокировочную муфту между любыми двумя звеньями планетарного ряда (рис.5), то при ее включении планетарный ряд будет заблокирован, и его передаточное отношение будет равно 1.
3. Отсюда вытекает известное свойство блокировки планетарного ряда: если установить блокировочную муфту между любыми двумя звеньями планетарного ряда (рис.5), то при ее включении планетарный ряд будет заблокирован, и его передаточное отношение будет равно 1.
| Рис.5 | 1 - малое центральное колесо; | 3 - водило; |
| 2 - большое центральное колесо; | 4 - блокировочная муфта |
Рассмотрим это свойство на примере планетарного ряда второго класса, т.е. с отрицательным внутренним передаточным отношением (i12<0). Здесь возможны два варианта.
Первый. Пусть большое центральное колесо будет остановлено ( 2=0), водило назначим ведомым звеном планетарного ряда, а малое центральное колесо - ведущим звеном (рис.6а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
2=0), водило назначим ведомым звеном планетарного ряда, а малое центральное колесо - ведущим звеном (рис.6а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
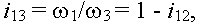
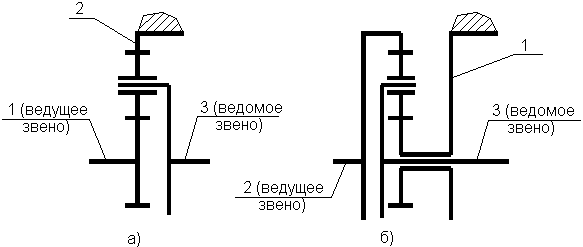
| Рис.6 | Варианты работы планетарного ряда в режиме редуктора. |
т.е. получаем редуктор, передаточное отношение которого на единицу больше внутреннего передаточного отношения самого планетарного ряда.
Второй. Пусть большое центральное колесо будет ведущим звеном планетарного ряда, водило - ведомым звеном, а малое центральное колесо - остановлено, (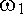 =0) (рис.6б). Тогда после небольшого преобразования (1) получим:
=0) (рис.6б). Тогда после небольшого преобразования (1) получим:
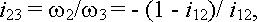
т.е. получаем редуктор, передаточное отношение которого близко к единице.
3. Свойство работать в режиме повышающей передачи. Опять-таки, рассмотрим это свойство на примере планетарного ряда второго класса, т.е. с отрицательным внутренним передаточным отношением (i12<0). Здесь также возможны два варианта.
Первый. Пусть большое центральное колесо будет остановлено (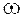 2=0), водило - ведущим звеном планетарного ряда, а малое центральное колесо - ведомым звеном (рис.7а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
2=0), водило - ведущим звеном планетарного ряда, а малое центральное колесо - ведомым звеном (рис.7а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
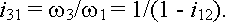
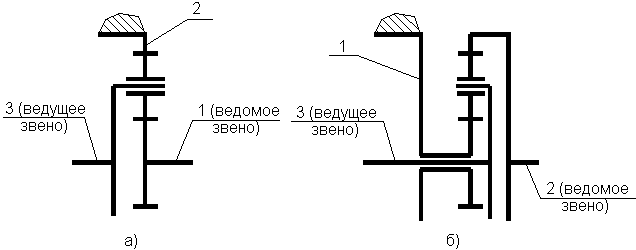
| Рис.7 | Варианты работы планетарного ряда в режиме повышающей передачи. |
Второй. Пусть большое центральное колесо будет ведомым звеном планетарного ряда, водило - ведущим звеном планетарного ряда, а малое центральное колесо - остановлено ( 1=0) (рис.7б). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
1=0) (рис.7б). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:
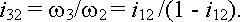
Анализ полученной зависимости показывает, что в этом случае будет получена повышающая передача с передаточным отношением близким к единице.
|
|
|
Дата добавления: 2015-05-10; Просмотров: 477; Нарушение авторских прав?; Мы поможем в написании вашей работы!