Библиографический список. Задание для самостоятельной работы по оцениванию параметров и проверке гипотезы о нормальном законе распределения

Задание для самостоятельной работы по оцениванию параметров и проверке гипотезы о нормальном законе распределения.

Проверка гипотезы о нормальном законе распределения по критерию Романовского.

Используя величину 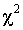, Романовский предложил оценивать близость эмпирического распределения кривой нормального распределения при помощи отношения

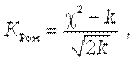
где m - число групп; k = (m - 3) - число степеней свободы при исчислении частот нормального распределения.

Если вышеуказанное отношение меньше 3, то расхождения эмпирических и теоретических частот можно считать случайными, а эмпирическое распределение - соответствующим нормальному. Если отношение больше 3, то расхождения могут быть достаточно существенными и гипотезу о нормальном распределении следует отвергнуть.

В нашем примере эмпирическое распределение соответствует нормальному.

По выборочным данным, представленным в заданиях №1 – №10, требуется:

1) построить интервальный вариационный ряд распределения;

2) вычислить выборочные характеристики по вариационному ряду: среднее выборочное значение, центральные моменты, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса, медиану, моду, коэффициент вариации;

3) построить гистограмму, полигон и кумуляту;

4) сделать вывод о форме ряда распределения по виду гистограммы и полигона, а также по значениям коэффициентов асимметрии и эксцесса;

5) рассчитать плотность и интегральную функцию теоретического распределения и построить эти кривые на графиках гистограммы и кумуляты соответственно;

6) проверить гипотезу о нормальном распределении по критерию согласия Пирсона и критерию Романовского.

№1. Предел прочности при сжатии 100 контрольных образцов бетона составил (МПа):

99,4 102,9 102,9 99,4 100,0 99,4 100,7 100,0 100,7

98,4 97,1 103,7 102,3 103,4 101,5 97,8 99,0 101,5

98,4 98,4 101,5 102,0 100,7 99,0 99,4 98,4 102,9 103,4

101,5 99,4 98,4 100,7 102,3 102,0 101,5 100,7 102,0 100,7

101,5 103,7 104,3 100,0 102,3 102,0 100,7 101,5 97,1 97,8

96,8 102,9 100,0 100,7 98,4 102,9 102,0 100,7 100,7 101,5

102,3 102,3 102,0 103,4 100,0 100,0 101,5 101,5 100,0 100,0

100,7 103,7 105,2 100,0 100,7 97,8 103,4 102,0 101,5 103,4

102,0 101,5 99,4 100,7 100,7 101,5 102,9 104,3 100,7 100,7

102,3 103,7 99,0 100,0 101,5 102,0 102,3 102,3 99,4 99,0

№2. Контрольные измерения коэффициента влажности песка для приготовления бетонной смеси в течение 100 дней показали следующие результаты:

0,55 0,80 0,80 0,79 0,62 0,59 0,93 0,66 0,75 0,07

0,47 1,12 0,75 0,63 0,15 0,81 0,97 0,86 0,59 0,40

0,98 0,36 0,88 0,69 0,98 0,72 0,38 0,26 0,70 0,58

0,25 0,85 0,94 0,25 0,77 0,26 0,67 0,62 0,42 0,95

0,62 0,45 0,75 1,10 0,36 0,16 0,77 0,58 0,60 0,29

0,71 0,85 1,11 0,65 0,58 0,05 0,34 0,57 0,18 0,78

0,87 0,88 0,65 1,01 0,60 0,78 0,68 0,84 0,82 0,07

0,21 0,77 0,68 0,87 0,42 0,43 1,14 0,20 0,82 0,44

0,73 0,48 0,87 0,60 0,12 0,44 0,91 0,77 0,31 0,85

0,74 0,69 0,51 0,36 0,92 0,61 0,81 0,51 0,49 0,46

№3. Предел прочности при сжатии 100 контрольных образцов бетона составил (МПа):

№4. Предел прочности при сжатии 100 контрольных образцов бетона составил (МПа):

40,1 66,8 46,7 58,5 54,0 66,8 54,5 89,5 34,7 33,9

52,3 76,5 55,5 52,2 54,3 44,7 53,5 46,5 66,8 50,5

89,5 49,5 55,6 52,3 48,3 49,5 47,3 54,0 51,3 23,5

66,8 66,8 76,5 26,3 40,3 51,4 58,3 32,4 76,5 91,4

34,4 45,5 50,6 66,8 22,8 76,5 44,9 41,1 34,1 76,5

33,7 50,1 45,5 50,1 51,6 66,8 76,5 76,5 48,4

54,0 34,5 20,1 34,5 66,3 40,5 55,8 49,1 66,8 89,5

25,1 91,4 22,3 34,5 47,1 76,5 89,5 51,5 54,5 58,3

47,5 92,2 92,2 38,9 51,1 34,6 40,5 76,5 66,8 44,5

50,8 49,8 66,8 92,2 89,5 20,1 33,9 34,8 41,1 45,6

№5. Предел прочности при изгибе 100 контрольных образцов бетона составил (МПа):

5,9 11,6 9,2 4,1 3,3 2,3 3,9 9,2 0,87 9,2

5,9 5,9 3,9 7,9 6,2 5,9 3,2 8,1 0,84 11,6

5,9 9,2 3,9 10,2 2,3 7,9 1,2 3,9 7,9 3,9

8,1 5,9 6,2 7,9 3,9 4,1 4,1 1,2 3,9 10,6

3,9 5,9 0,3 4,1 0,3 5,0 4,8 5,2 5,9 10,6

4,1 5,9 2,9 4,9 1,2 5,9 3,4 4,8 6,4 4,1

4,1 4,1 3,8 2,8 3,9 4,3 5,3 3,9 5,1 6,4

4,1 5,9 4,3 7,8 7,9 10,6 4,7 4,8 10,6 3,9

6,1 5,9 4,8 3,9 4,1 10,6 9,2 4,9 6,3 4,1

11,6 2,3 4,1 7,9 2,7 2,3 4,1 1,2 9,2 1,8

№6. Контрольные измерения коэффициента химической стойкости 100 контрольных образцов бетона дали следующие результаты:

0,54 0,43 0,43 0,47 0,21 0,58 0,47 0,68 0,54 0,37

0,64 0,43 0,43 0,61 0,43 0,68 0,64 0,47 0,47 0,43

0,33 0,27 0,64 0,47 0,11 0,33 0,43 0,47 0,27 0,43

0,61 0,21 0,54 0,54 0,47 0,43 0,43 0,68 0,27 0,05

0,47 0,54 0,21 0,61 0,71 0,33 0,33 0,43 0,21 0,37

0,79 0,54 0,64 0,27 0,11 0,54 0,37 0,54 0,43 0,33

0,33 0,79 0,64 0,39 0,64 0,11 0,47 0,43 0,33 0,33

0,58 0,47 0,08 0,79 0,33 0,27 0,47 0,33 0,54 0,54

0,40 0,47 0,47 0,71 0,08 0,21 0,27 0,54 0,54 0,33

0,43 0,43 0,47 0,40 0,85 0,33 0,68 0,33 0,54 0,27

№7. Время сборки трубопроводного вентиля (сек.) на конвейере следующее:

12,54 12,55 12,94 12,77 13,21 13,60 13,21 12,92 13,75 12,98

12,76 12,89 13,41 13,25 13,30 13,09 12,59 13,08 12,94 13,18

13,35 12,83 13,22 12,83 13,17 13,26 12,65 13,01 13,00 13,29

13,21 13,07 13,18 13,05 12,84 12,85 12,74 12,88 13,32 12,57

12,98 13,15 13,41 13,32 13,36 13,70 12,87 13,51 13,05 13,60

12,95 13,11 12,66 13,76 13,22 12,88 13,47 13,39 13,82 13,22

12,92 13,10 13,08 12,86 12,84 13,27 13,27 12,82 13,76 13,16

13,13 13,01 13,10 12,93 12,98 13,55 13,34 13,03 12,78 13,00

13,92 13,20 13,29 13,16 13,41 12,91 13,22 13,18 12,72 13,32

12,57 13,28 13,79 13,15 12,78 13,90 12,65 13,61 13,27 13,20

№8. Расход меди (гр.) на изготовление трубопроводного вентиля составил:

109,6 106,8 110,3 106,7 104,5 116,6 114,9 113,3 110,4 110,8

112,6 106,9 114,5 108,9 108,6 107,9 110,8 106,3 107,1 104,7

112,6 113,4 109,1 111,4 108,6 106,1 107,3 112,9 107,8 104,1

111,2 104,1 112,0 110,4 111,9 109,6 105,1 109,7 110,0 105,0

109,5 111,8 110,2 111,2 110,8 112,6 109,4 113,5 111,2 107,4

113,3 104,0 106,5 107,3 116,6 107,3 107,2 113,6 111,8 112,9

111,0 110,3 106,9 106,9 106,4 113,3 107,6 108,6 108,6 108,6

116,8 109,7 111,3 108,6 109,9 107,8 112,1 109,2 111,6 110,9

108,7 109,4 104,7 105,3 112,1 110,2 109,9 111,0 107,9 110,9

115,7 106,9 110,3 113,4 112,3 115,5 110,8 114,7 108,6 107,3

№9. Время сборки электродвигателя общего назначения (сек.) на конвейере следующее:

102,0 104,7 102,8 102,6 104,3 101,1 100,8 102,0 103,9 101,8

108,4 107,8 103,5 101,2 103,1 101,9 101,8 103,5 103,3 104,8

106,9 107,1 102,9 104,4 103,1 101,5 101,3 103,7 101,8 105,3

104,6 101,2 103,9 102,7 105,2 104,9 102,8 108,3 103,7 100,8

103,6 101,5 101,5 103,8 105,2 105,2 104,3 104,9 104,2 103,8

105,3 102,8 105,5 102,6 101,9 102,3 105,3 103,3 101,0 106,4

101,8 106,7 103,9 103,6 104,6 104,3 103,1 103,9 100,2 109,6

101,2 102,0 105,1 103,3 106,2 105,6 103,4 106,2 100,5 102,7

102,7 105,4 104,6 102,8 103,2 102,5 104,7 104,9 105,9 101,2

105,7 102,3 102,8 102,3 102,2 101,6 106,2 105,3 104,2 105,3

№10. Затраты цветных металлов на изготовление одного промышленного светильника (гр.) составили:

101,6 93,7

91,6 91,1 89,3 93,2

101,1 89,1 95,2 93,5 95,1 95,9

98,5 86,3 95,7 98,2 95,8

95,2 86,8

104,2 93,9 93,4 95,5 98,8

92,6

91,9 96,8 89,9 98,7 89,6 93,2 95,6 95,6

95,7

76,3 91,8 87,4 93,5

Приложение

Таблица значений функции Лапласа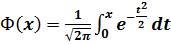

x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)
0,00	0,0000	0,50	0,1915	1,00	0,3413	1,50	0,4332	2,00	0,4772	3,00	0,49865
0,01	0,0040	0,51	0,1950	1,01	0,3438	1,51	0,4345	2,02	0,4783	3,20	0,49931
0,02	0,0080	0,52	0,1985	1,02	0,3461	1,52	0,4357	2,04	0,4793	3,40	0,49966
0,03	0,0120	0,53	0,2019	1,03	0,3485	1,53	0,4370	2,06	0,4803	3,60	0,499841
0,04	0,0160	0,54	0,2054	1,04	0,3508	1,54	0,4382	2,08	0,4812	3,80	0,499928
0,05	0,0199	0,55	0,2088	1,05	0,3531	1,55	0,4394	2,10	0,4821	4,00	0,499968
0,06	0,0239	0,56	0,2123	1,06	0,3554	1,56	0,4406	2,12	0,4830	4,50	0,499997
0,07	0,0279	0,57	0,2157	1,07	0,3577	1,57	0,4418	2,14	0,4838	5,00	0,499997
0,08	0,0319	0,58	0,2190	1,08	0,3599	1,58	0,4429	2,16	0,4846
0,09	0,0359	0,59	0,2224	1,09	0,3621	1,59	0,4441	2,18	0,4854
0,10	0,0398	0,60	0,2257	1,10	0,3643	1,60	0,4452	2,20	0,4861
0,11	0,0438	0,61	0,2291	1,11	0,3665	1,61	0,4463	2,22	0,4868
0,12	0,0478	0,62	0,2324	1,12	0,3686	1,62	0,4474	2,24	0,4875
0,13	0,0517	0,63	0,2357	1,13	0,3708	1,63	0,4484	2,26	0,4881
0,14	0,0557	0,64	0,2389	1,14	0,3729	1,64	0,4495	2,28	0,4887
0,15	0,0596	0,65	0,2422	1,15	0,3749	1,65	0,4505	2,30	0,4893
0,16	0,0636	0,66	0,2454	1,16	0,3770	1,66	0,4515	2,32	0,4898
0,17	0,0675	0,67	0,2486	1,17	0,3790	1,67	0,4525	2,34	0,4904
0,18	0,0714	0,68	0,2517	1,18	0,3810	1,68	0,4535	2,36	0,4909
0,19	0,0753	0,69	0,2549	1,19	0,3830	1,69	0,4545	2,38	0,4913
0,20	0,0793	0,70	0,2580	1,20	0,3849	1,70	0,4554	2,40	0,4918
0,21	0,0832	0,71	0,2611	1,21	0,3869	1,71	0,4564	2,42	0,4922
0,22	0,0871	0,72	0,2642	1,22	0,3883	1,72	0,4573	2,44	0,4927
0,23	0,0910	0,73	0,2673	1,23	0,3907	1,73	0,4582	2,46	0,4931
0,24	0,0948	0,74	0,2703	1,24	0,3925	1,74	0,4591	2,48	0,4934
0,25	0,0987	0,75	0,2734	1,25	0,3944	1,75	0,4599	2,50	0,4938
0,26	0,1026	0,76	0,2764	1,26	0,3962	1,76	0,4608	2,52	0,4941
0,27	0,1064	0,77	0,2794	1,27	0,3980	1,77	0,4616	2,54	0,4945
0,28	0,1103	0,78	0,2823	1,28	0,3997	1,78	0,4625	2,56	0,4948
0,29	0,1141	0,79	0,2852	1,29	0,4015	1,79	0,4633	2,58	0,4951
0,30	0,1179	0,80	0,2881	1,30	0,4032	1,80	0,4641	2,60	0,4953
0,31	0,1217	0,81	0,2910	1,31	0,4049	1,81	0,4649	2,62	0,4956
0,32	0,1255	0,82	0,2939	1,32	0,4066	1,82	0,4656	2,64	0,4959
0,33	0,1293	0,83	0,2967	1,33	0,4082	1,83	0,4664	2,66	0,4961
0,34	0,1331	0,84	0,2995	1,34	0,4099	1,84	0,4671	2,68	0,4963
0,35	0,1368	0,85	0,3023	1,35	0,4115	1,85	0,4678	2,70	0,4965
0,36	0,1406	0,86	0,3051	1,36	0,4131	1,86	0,4686	2,72	0,4967
0,37	0,1443	0,87	0,3078	1,37	0,4147	1,87	0,4693	2,74	0,4969
0,38	0,1480	0,88	0,3106	1,38	0,4162	1,88	0,4699	2,76	0,4971
0,39	0,1517	0,89	0,3133	1,39	0,4177	1,89	0,4706	2,78	0,4973
0,40	0,1554	0,90	0,3159	1,40	0,4192	1,90	0,4713	2,80	0,4974
0,41	0,1591	0,91	0,3186	1,41	0,4207	1,91	0,4719	2,82	0,4976
0,42	0,1628	0,92	0,3212	1,42	0,4222	1,92	0,4726	2,84	0,4977
0,43	0,1664	0,93	0,3238	1,43	0,4236	1,93	0,4732	2,86	0,4979
0,44	0,1700	0,94	0,3264	1,44	0,4251	1,94	0,4738	2,88	0,4980
0,45	0,1736	0,95	0,3289	1,45	0,4265	1,95	0,4744	2,90	0,4981
0,46	0,1772	0,96	0,3315	1,46	0,4279	1,96	0,4750	2,92	0,4982
0,47	0,1808	0,97	0,3340	1,47	0,4292	1,97	0,4756	2,94	0,4984
0,48	0,1844	0,98	0,3365	1,48	0,4306	1,98	0,4761	2,96	0,4985
0,49	0,1879	0,99	0,3389	1,49	0,4319	1,99	0,4767	2,98	0,4986

Таблица критических точек распределения Пирсона

k /α	0,01	0,025	0,05	0,95	0,975	0,99
	6,63490	5,02389	3,84146	0,00393	0,00098	0,00016
	9,21034	7,37776	5,99146	0,10259	0,05064	0,02010
	11,34487	9,34840	7,81473	0,35185	0,21580	0,11483
	13,2767	11,14329	9,48773	0,71072	0,48442	0,29711
	15,08627	12,8325	11,0705	1,14548	0,83121	0,55430
	16,81189	14,44938	12,59159	1,63538	1,23734	0,87209
	18,47531	16,01276	14,06714	2,16735	1,68987	1,23904
	20,09024	17,53455	15,50731	2,73264	2,17973	1,64650
	21,66599	19,02277	16,91898	3,32511	2,70039	2,08790
	23,20925	20,48318	18,30704	3,94030	3,24697	2,55821
	24,72497	21,92005	19,67514	4,57481	3,81575	3,05348
	26,21697	23,33666	21,02607	5,22603	4,40379	3,57057
	27,68825	24,7356	22,36203	5,89186	5,00875	4,10692
	29,14124	26,11895	23,68479	6,57063	5,62873	4,66043
	30,57791	27,48839	24,99579	7,26094	6,26214	5,22935
	31,99993	28,84535	26,29623	7,96165	6,90766	5,81221
	33,40866	30,19101	27,58711	8,67176	7,56419	6,40776
	34,80531	31,52638	28,86930	9,39046	8,23075	7,01491
	36,19087	32,85233	30,14353	10,11701	8,90652	7,63273
	37,56623	34,16961	31,41043	10,85081	9,59078	8,26040
	38,93217	35,47888	32,67057	11,59131	10,2829	8,89720
	40,28936	36,78071	33,92444	12,33801	10,98232	9,54249
	41,63840	38,07563	35,17246	13,09051	11,68855	10,19572
	42,97982	39,36408	36,41503	13,84843	12,40115	10,85636
	44,31410	40,64647	37,65248	14,61141	13,11972	11,52398
	45,64168	41,92317	38,88514	15,37916	13,84391	12,19815
	46,96294	43,19451	40,11327	16,15140	14,57338	12,87850
	48,27824	44,46079	41,33714	16,92788	15,30786	13,56471
	49,58788	45,72229	42,55697	17,70837	16,04707	14,25645
	50,89218	46,97924	43,77297	18,49266	16,79077	14,95346
	52,19139	48,23189	44,98534	19,28057	17,53874	15,65546
	53,48577	49,48044	46,19426	20,07191	18,29076	16,36222
	54,77554	50,72508	47,39988	20,86653	19,04666	17,07351
	56,06091	51,96600	48,60237	21,66428	19,80625	17,78915
	57,34207	53,20335	49,80185	22,46502	20,56938	18,50893
	58,61921	54,43729	50,99846	23,26861	21,33588	19,23268
	59,89250	55,66797	52,19232	24,07494	22,10563	19,96023
	61,16209	56,89552	53,38354	24,8839	22,87848	20,69144
	62,42812	58,12006	54,57223	25,69539	23,65432	21,42616
	63,69074	59,34171	55,75848	26,5093	24,43304	22,16426
	64,95007	60,56057	56,94239	27,32555	25,21452	22,90561
	66,20624	61,77676	58,12404	28,14405	25,99866	23,65009
	67,45935	62,99036	59,30351	28,96472	26,78537	24,39760
	68,70951	64,20146	60,48089	29,78748	27,57457	25,14803
	69,95683	65,41016	61,65623	30,61226	28,36615	25,90127
	71,20140	66,61653	62,82962	31,43900	29,16005	26,65724
	72,44331	67,82065	64,00111	32,26762	29,95620	27,41585
	73,68264	69,02259	65,17077	33,09808	30,75451	28,17701
	74,91947	70,22241	66,33865	33,93031	31,55492	28,94065
	76,15389	71,42020	67,50481	34,76425	32,35736	29,70668

1. Гмурман В. Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 2004 г. – 478 с. – (Высшее образование).

2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистики.- М.: Высшая школа, 2004 г. – 404 с. – (Высшее образование).

3. Письменный Д. Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам.- М.: Айрис-пресс, 2006 г. – 288 с. – (Высшее образование).

4. Клячкин В. Н. Статистические методы в управлении качеством: компьютерные технологии: учеб. пособие.- М.: Финансы и статистика; ИНФРА-М, 2009. – 304 с.: ил.

5. Шишкин И.Ф. Контроль: Учебное пособие. – Санкт-Петербург: СЗПИ, 1992.

Дата добавления: 2015-05-10