Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

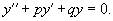
Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:

Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод вариации постоянных

Если общее решение y0 однородного уравнения известно, то частное решение y1 для соответствующего неоднородного уравнения можно найти, используя метод вариации постоянных.

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

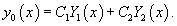
Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).

Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:

Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1)

2)

где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.

В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель , где s − порядок корня α в характеристическом уравнении.

В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.

Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Принцип суперпозиции

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида

то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

Пример 1

Решить дифференциальное уравнение y'' + y = sin(2x)

Решение.

Сначала мы решим соответствующее однородное уравнение y'' + y = 0. В данном случае корни характеристического уравнения являтся чисто мнимыми:

Следовательно, общее решение однородного уравнения определяется выражением

Вернемся снова к неоднородному уравнению. Будем искать его решение в виде

используя метод вариации постояных.

Функции C1(x) и C2(x) можно найти из следующей системы уравнений:

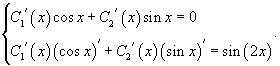
Тогда

Выразим производную 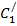(x) из первого уравнения:

Подставляя во второе уравнение, находим производную ' (x):

Отсюда следует, что

Интегрируя выражения для производных C1' (x) и C2' (x), получаем:

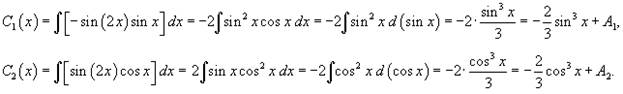
где A1, A2 − постоянные интегрирования.

Теперь подставим найденные функции C1(x) и C2(x) в формулу для y1(x) и запишем общее решение неоднородного уравнения:

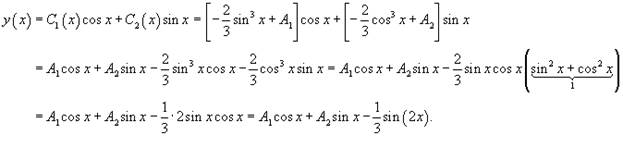
Дата добавления: 2015-05-10