Исследование операций в экономике 2 страница

x₂ = 45.02-0x₃+0.00948x₈+0x₁₁-0.00948x₁₂-0x₁₅

В качестве новой переменной выбираем x₈.

Вычислим значения D_i по всем уравнениям для этой переменной: b_i / a_i8

и из них выберем наименьшее:

Вместо переменной x₁₄ в план войдет переменная x₈.

Выразим переменную x₈ через x₁₄

и подставим во все выражения.

После приведения всех подобных, получаем новую систему, эквивалентную прежней:

x₀ = -1E-06-0x₃-0x₆-0x₉-0x₁₀-0x₁₁-x₁₂-1x₁₃-1x₁₄-1x₁₅

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁+0x₁₃-0.44x₁₄+0x₁₅

x₇ = 50556.23-11.54x₃-133.74x₆-16.08x₉-124.94x₁₀-12.04x₁₁+16.08x₁₃+124.94x₁₄+12.04x₁₅

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁-0.0291x₁₃-0x₁₄-0x₁₅

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁+0.07x₁₃+0.45x₁₄+0.0741x₁₅

x₈ = 7959.25+8.6x₃+93x₆+7.38x₉+47.93x₁₀+7.81x₁₁+x₁₂-7.38x₁₃-47.93x₁₄-7.81x₁₅

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁-0.07x₁₃-0.45x₁₄-0.0741x₁₅

Полагая небазисные переменные x = (5, 7, 4, 1, 8, 2) равными нулю, получим новый допустимый вектор и значение целевой функции:

x = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1), x₀ = -1E-06

Выражение для x₀ не содержит положительных элементов. Найден оптимальный план.

x₀ = -1E-06-0x₃-0x₆-0x₉-0x₁₀-0x₁₁-x₁₂-1x₁₃-1x₁₄-1x₁₅

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁+0x₁₃-0.44x₁₄+0x₁₅

x₇ = 50556.23-11.54x₃-133.74x₆-16.08x₉-124.94x₁₀-12.04x₁₁+16.08x₁₃+124.94x₁₄+12.04x₁₅

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁-0.0291x₁₃-0x₁₄-0x₁₅

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁+0.07x₁₃+0.45x₁₄+0.0741x₁₅

x₈ = 7959.25+8.6x₃+93x₆+7.38x₉+47.93x₁₀+7.81x₁₁+x₁₂-7.38x₁₃-47.93x₁₄-7.81x₁₅

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁-0.07x₁₃-0.45x₁₄-0.0741x₁₅

На этом первый этап симплекс-метода завершен. Переходим ко второму этапу. Удаляем переменные с искусственными переменными.

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁

x₇ = 50556.23-11.54x₃-133.74x₆-16.08x₉-124.94x₁₀-12.04x₁₁

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁

x₈ = 7959.25+8.6x₃+93x₆+7.38x₉+47.93x₁₀+7.81x₁₁

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁

Выразим базисные переменные:

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁

которые подставим в целевую функцию:

F(X) = 57293.83+4.9x₃+31.96x₆+3.42x₉+21.39x₁₀+3.09x₁₁

Получаем новую систему переменных.

x₀ = 57293.83+4.9x₃+31.96x₆+3.42x₉+21.39x₁₀+3.09x₁₁

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁

x₇ = 50556.23-11.54x₃-133.74x₆-16.08x₉-124.94x₁₀-12.04x₁₁

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁

x₈ = 7959.25+8.6x₃+93x₆+7.38x₉+47.93x₁₀+7.81x₁₁

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁

max(0,0,4.9,0,0,31.96,0,0,3.42,21.39,3.09) = 31.96

x₀ = 57293.83+4.9x₃+31.96x₆+3.42x₉+21.39x₁₀+3.09x₁₁

x₅ = 1800-0x₃-0x₆-0x₉+0.44x₁₀-0x₁₁

x₇ = 50556.23-11.54x₃-133.74x₆-16.08x₉-124.94x₁₀-12.04x₁₁

x₄ = 1087.21+0x₃+0x₆+0.0291x₉+0x₁₀+0x₁₁

x₁ = 4799.53-1.08x₃-1.88x₆-0.07x₉-0.45x₁₀-0.0741x₁₁

x₈ = 7959.25+8.6x₃+93x₆+7.38x₉+47.93x₁₀+7.81x₁₁

x₂ = 120.47+0.0815x₃+0.88x₆+0.07x₉+0.45x₁₀+0.0741x₁₁

В качестве новой переменной выбираем x₆.

Вычислим значения D_i по всем уравнениям для этой переменной: b_i / a_i6

и из них выберем наименьшее:

Вместо переменной x₇ в план войдет переменная x₆.

Выразим переменную x₆ через x₇

и подставим во все выражения.

После приведения всех подобных, получаем новую систему, эквивалентную прежней:

x₀ = 69374.4+2.14x₃-0.24x₇-0.42x₉-8.46x₁₀+0.21x₁₁

x₅ = 1800-0x₃-0x₉+0.44x₁₀-0x₁₁

x₆ = 378.02-0.0863x₃-0.00748x₇-0.12x₉-0.93x₁₀-0.09x₁₁

x₄ = 1087.21+0x₃+0.0291x₉-0x₁₀-0x₁₁

x₁ = 4088.3-0.92x₃+0.0141x₇+0.16x₉+1.3x₁₀+0.0953x₁₁

x₈ = 43113.4+0.57x₃-0.7x₇-3.8x₉-38.94x₁₀-0.56x₁₁

x₂ = 453.68+0.00542x₃-0.00659x₇-0.036x₉-0.37x₁₀-0.00526x₁₁

Полагая небазисные переменные x = (5, 6, 4, 1, 8, 2) равными нулю, получим новый допустимый вектор и значение целевой функции:

x = (0, 0, -2.14, 0, 0, 0, 0.24, 0, 0.42, 8.46, -0.21), x₀ = 69374.4

max(0,0,2.14,0,0,0,-0.24,0,-0.42,-8.46,0.21) = 2.14

x₀ = 69374.4+2.14x₃-0.24x₇-0.42x₉-8.46x₁₀+0.21x₁₁

x₅ = 1800-0x₃-0x₉+0.44x₁₀-0x₁₁

x₆ = 378.02-0.0863x₃-0.00748x₇-0.12x₉-0.93x₁₀-0.09x₁₁

x₄ = 1087.21+0x₃+0.0291x₉-0x₁₀-0x₁₁

x₁ = 4088.3-0.92x₃+0.0141x₇+0.16x₉+1.3x₁₀+0.0953x₁₁

x₈ = 43113.4+0.57x₃-0.7x₇-3.8x₉-38.94x₁₀-0.56x₁₁

x₂ = 453.68+0.00542x₃-0.00659x₇-0.036x₉-0.37x₁₀-0.00526x₁₁

В качестве новой переменной выбираем x₃.

Вычислим значения D_i по всем уравнениям для этой переменной: b_i / a_i3

и из них выберем наименьшее:

Вместо переменной x₆ в план войдет переменная x₃.

Выразим переменную x₃ через x₆

и подставим во все выражения.

После приведения всех подобных, получаем новую систему, эквивалентную прежней:

x₀ = 78749.4-24.8x₆-0.42x₇-3.41x₉-31.63x₁₀-2.02x₁₁

x₅ = 1800+0x₆+0.44x₁₀

x₃ = 4380.67-11.59x₆-0.0866x₇-1.39x₉-10.83x₁₀-1.04x₁₁

x₄ = 1087.21-0x₆+0.0291x₉-0x₁₀-0x₁₁

x₁ = 61.91+10.65x₆+0.0937x₇+1.44x₉+11.25x₁₀+1.05x₁₁

x₈ = 45616.83-6.62x₆-0.74x₇-4.6x₉-45.13x₁₀-1.15x₁₁

x₂ = 477.41-0.0628x₆-0.00706x₇-0.0436x₉-0.43x₁₀-0.0109x₁₁

Полагая небазисные переменные x = (5, 3, 4, 1, 8, 2) равными нулю, получим новый допустимый вектор и значение целевой функции:

x = (0, 0, 0, 0, 0, 24.8, 0.42, 0, 3.41, 31.63, 2.02), x₀ = 78749.4

Выражение для x₀ не содержит положительных элементов. Найден оптимальный план.

Окончательный вариант системы уравнений:

x₀ = 78749.4-24.8x₆-0.42x₇-3.41x₉-31.63x₁₀-2.02x₁₁

x₅ = 1800+0x₆+0.44x₁₀

x₃ = 4380.67-11.59x₆-0.0866x₇-1.39x₉-10.83x₁₀-1.04x₁₁

x₄ = 1087.21-0x₆+0.0291x₉-0x₁₀-0x₁₁

x₁ = 61.91+10.65x₆+0.0937x₇+1.44x₉+11.25x₁₀+1.05x₁₁

x₈ = 45616.83-6.62x₆-0.74x₇-4.6x₉-45.13x₁₀-1.15x₁₁

x₂ = 477.41-0.0628x₆-0.00706x₇-0.0436x₉-0.43x₁₀-0.0109x₁₁

Оптимальный план можно записать так:

x₅ = 1800

x₃ = 4380.67

x₄ = 1087.21

x₁ = 61.91

x₈ = 45616.83

x₂ = 477.41

F(X) = 4.8*61.91 + 46.5*477.41 + 6.3*4380.67 + 17.25*1087.21 + 5.5*1800 = 78749.4

Согласно оптимальному решению, максимальный выход валовой продукции в денежном выражении, равный 78749.4 тыс. руб., обеспечит следующая структура производства (Приложение 3):

х₂- 477 га картофеля,

х₃- 4380 га многолетних трав,

х₄- 1087 голов дойного стада,

х₅- 1800 головы молодняка КРС.

Оценки основных небазисных здесь отсутствуют, так как все четыре исходных отраслей вошли в оптимальный план задачи. Судя по оценкам ограничений, дефицитными ресурсами являются пашня и трудовые ресурсы. При недоиспользовании площади пашни на 1 га целевая функция уменьшится на 27,059 тыс. руб., а при недоиспользовании труда на 1 чел.-час. ее значение снизится по сравнению с оптимальным на 345,12 руб. Следует добавить, что при решении больших моделей, адекватных реальным условиям сельскохозяйственного производства, площадь пашни действительно должна быть полностью востребованной, чего явно некорректно ожидать от уровня использования труда; иначе вводятся условия по его привлечению, как в целом, так и в пиковые по потребности периоды сельскохозяйственных работ. При реализации дополнительно 1 ц молока целевая функция уменьшится на 4228,51 руб., а при продаже сверхпланового центнера прироста – на 42,322 тыс. руб. за счет менее эффективного альтернативного способа использования производственных ресурсов (пашня и труд). Таким образом, производство экономически невыгодной продукции без государственного дотирования по влиянию на валовую выручку равнозначно значительному недоиспользованию дефицитных ресурсов. Аналогично этому, превышение выхода кормов над реальной потребностью в них без должного учета и контроля над их использованием и/или неподкрепленное приростом удельного выхода продукции животноводства в натуральном и денежном выражении (низкопородный скот) также ощутимо снижает результаты деятельности сельскохозяйственного предприятия. Согласно анализу дополнительных базисных переменных, экономически выгодными являются производство зерна и картофеля, а не выгодной, но запланированной, возможно, в пределах дотаций или договоров продукцией - производство молока и прироста.

Задача 3

Общая сумма кредитов банковского филиала 3640 тыс. руб. Необходимая информация представлена в следующей таблице.

Субъекты кредитования	Нижняя граница кредитования, %	Верхняя граница кредитования, %	Кредитная ставка, %
Юридические лица Предприниматели Другие банки Работники банка			19,5

Сформировать оптимальную структуру кредитования, обеспечивающую максимальную прибыль от размещения кредитов.

Решение:

а) Переменные задачи:

х₁- кредиты юридическим лицам, тыс. руб.;

х₂- кредиты предпринимателям, тыс. руб.;

х₃- межбанковские кредиты, тыс. руб.;

х₄- кредиты работникам банка, тыс. руб.

б) Система ограничений:

1) по общей сумме кредитов, тыс. руб.

;

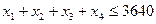2) по минимальной доле юридических лиц, тыс. руб.

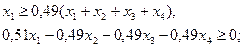
3) по максимальной доле юридических лиц, тыс. руб.

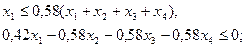
4) по минимальной доле предпринимателей, тыс. руб.

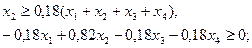
5) по максимальной доле предпринимателей, тыс. руб.

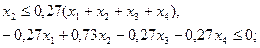
6) по минимальной доле межбанковского кредита, тыс. руб.

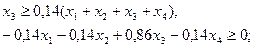
7) по максимальной доле межбанковского кредита, тыс. руб.

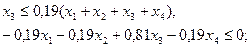
8) по минимальной доле работников банка, тыс. руб.

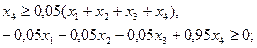
9) по максимальной доле работников банка, тыс. руб.

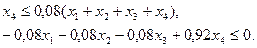
в) Целевая функция:

.

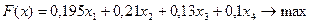x₁ (кредиты юридическим лицам)= 1965.6 тыс. руб. или 54 %

x₂ (кредиты предпринимателям)= 982.8 тыс. руб. или 27 %

x₃ (межбанковские кредиты)= 509.6 тыс. руб. или 14%

x₄ (кредиты работникам банка)= 182 тыс. руб. или 5 %

F(X) = 0.195*1965.6 + 0.21*982.8 + 0.13*509.6 + 0.1*182 = 674.13

Разумеется, алгоритмом максимизации прибыли банка от размещения кредитов выбраны наиболее доходные вложения денежных средств. Возможно, в реальности стоит несколько увеличить долю работников банка за счет межбанковских кредитов или особенно кредитов юридическим лицам. Тем не менее, данное решение вполне имеет практическую значимость с точки зрения сочетания доходности и надежности кредитных вложений. При этом даже существенное изменение общей годовой суммы кредитов в принципе не повлияет на результат решенной задачи, т.к. в данном случае главное значение имеет найденная оптимальная структура кредитования. Основные небазисные переменные здесь отсутствуют, так как все виды выдаваемых кредитов обоснованно вошли в оптимальный план задачи, ибо по каждому из них существовала нижняя долевая граница. Так, если недовложить в кредиты в целом 1 тыс. руб., то значение целевой функции уменьшится на 185 руб. По сути, это и будет средневзвешенная кредитная ставка: 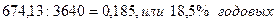. Если недовложить 1 тыс. руб. в кредиты предпринимателям, то целевая функция снизится на 0,21 тыс. руб., поскольку размер общей суммы кредитов выдерживается, и эта 1 тыс. руб. будет размещена среди юридических лиц – клиентов банка - под 18% годовых. Тогда 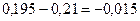. Если превысить максимальную долевую границу межбанковских кредитов на 1 тыс. руб., то размер целевой функции снизится на 0,13 тыс. руб., так как эта сумма автоматически изымается у юридических лиц с большей доходностью вложений: 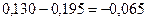. Если превысить минимальную границу кредитов работникам банка, то эта сумма изымается у юридических лиц, поскольку следующая по уровню доходности доля межбанковского кредита выдержана по минимуму и оттуда (во всяком случае, теоретически) брать средства куда-либо нельзя. Тогда 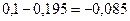- уменьшение значения целевой функции на 0,1тыс. руб.. Дефицитными ресурсами здесь можно условно назвать кредиты предпринимателям и кредитные средства в целом. Кстати, здесь легко заметить, что данный анализ является упрощенным аналогом рассмотренных в предыдущей задаче финансовых потоков в том смысле, что их доходности являются достаточно наглядными и не требуют специальных расчетов; именно поэтому в учебном процессе решение этой задачи предшествует четвертому заданию. Анализ дополнительных базисных переменных в данной задаче не обязателен, так как ограничения выполнены в структурной форме с использованием коэффициентов пропорциональности и приведены к нулевым объемам. К тому же анализ оптимального плана вложений и оценок ограничений полностью заменяют данный раздел решенной задачи.

Список литературы

• Заварыкин В.М. и др. Численные методы. - М.: Просвещение, 1991.
• Крутевский и др. Вычислительная техника в инженерных и экономических расчетах. - М.: Высшая школа, 1985.
• Информатика. Учебник. / Под ред. И.В.Макаровой. – 3-е изд.перераб. – М.: Финансы и статистика, 2005.
• Конюховский П.В. Математические методы исследования операций: пособие для подготовки к экзамену. – СПб.:Питер, 2001.
• Акулич И.Л. Математическое программирование в задачах и упражнениях. - М.: Высшая школа, 1993.
• Давыдов Э.Г. Исследование операций. – М. Высш. школа, 1990.
• Курицкий Б.К. Поиск оптимальных решений средствами Excel 7.0. - СПб.: BHV, 1997.
• Шикин Е.В. Чхартишвили А.Г. Математические методы и модели в управлении: Учебник для ВУЗов. - М.: Дело, 2000.
• Горелик В.А., Ушаков И.А. Исследование операций. - М.: Машиностроение, 1986.
• Вентцель Е.С. Исследование операций. - М.: Советское радио, 1972.
• Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. – М.: Наука,1965.
• Вагнер Г. Основы исследования операций. Т.1-3. - М. Мир, 1972,1973.
• Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука, 1980.
• Вилкас Э.И. Оптимальность в играх и решениях. - М.: Наука,1990.
• Гермейер Ю.Б. Введение в теорию исследования операций. - М.: Наука, 1976.
• Евтушенко Ю.Г. Методы решения экспериментальных задач и их применение в системах оптимизации. - М.: Наука, 1982.
• Интрилигатор М. Математические методы оптимизации и экономическая теория. - М.: Прогресс, 1975.
• Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. - М.: Высшая школа, 1986.
• Мулен Э. Теория игр с примерами из математической экономики. - М.: Мир, 1985. Павловский Ю.Н. Имитационные модели и системы. - М.: Фазиз, 2000.
• Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов. - М.: Высшая школа, Книжный дом «Университет», 1998.
• Таха Х. Введение в исследование операций. Т.1, 2. - М.: Мир, 1985.

Дата добавления: 2015-05-10