Вероятностный (энтропийный) подход

Измерение количества информации

Кодирование информации

Измерение количества информации.

М.Г. Юдина

Методические указания к самостоятельной работе

по курсу "Информатика"

Березники 2009

Составитель М.Г.Юдина

УДК 681.3.06

Ю 16

Рецензент канд.техн.наук, доцент кафедры химической технологии и экологии БФ ПГТУ С.В.Лановецкий.

Ю 16 Измерение количества информации. Кодирование информации: методические указания к самостоятельной работе по курсу "Информатика" для студентов технических специальностей / сост. М.Г.Юдина. - Перм.гос.техн.ун-т, Березниковский филиал, 2009. - 24 с.

Предназначены для оказания помощи студентам в практическом освоении подходов к измерению количества информации, кодирования числовой, текстовой и графической информации. Указания могут быть использованы для самостоятельного изучения систем счисления, способов представления чисел и выполнения арифметических действий над двоичными числами. Методические указания включают теоретическую часть, набор заданий для самостоятельного решения и контрольные вопросы по изучаемой теме.

Методические указания предназначены для студентов технических специальностей, обучающихся по очной и очно-заочной формам обучения.

Ó ГОУ ВПО

"Пермский государственный

технический университет",

Березниковский филиал, 2009

Определить понятие «количество информации» довольно сложно. В решении этой проблемы существует два основных подхода. Исторически они возникли почти одновременно. В конце 1940 года один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению информации, а работы по созданию ЭВМ привели к «объемному» подходу.

Рассмотрим опыт, связанный с бросанием правильной игральной кости, имеющей N граней. Результатом данного опыта может быть выпадение грани с одним из следующих знаков: 1, 2, …, N. Все N исходов этого опыта являются равновероятными.

Введем в рассмотрение численную величину (обозначим ее Н), опреде-ляющую количество информации, содержащее в сообщении о том, что произошло одно из N -равновероятных событий. Это величина называется энтропией и для ее вычисления используется формула Хартли

Н =log₂ N. (1)

Возьмем наиболее распространенный случай – бросание шестигранной кости, когда N= 6. В этом случае Н =log₂6=2,585, т.е. столько информации несет сообщение о выпадении одного из шести знаков игральной кости.

Решим еще один пример. Предположим, что нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: Н = log₂100» 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации приблизительно равное 6,644 единицы информации.

Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, H будет равно единице при N =2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны два исхода: «орел» и «решка»). Такая единица количества информации называется бит.

Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода, когда вероятности различных исходов неодинаковы (т.е. P_{i .} могут быть различны) используется формула Шеннона:

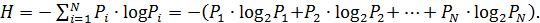(2)

Например, определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака «пробел» для разделения слов. По формуле (1)

H =log₂34»5,09 бит.

Однако в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. В табл. 1 приведены вероятности частоты употребления различных знаков русского алфавита, полученные на основе анализа очень больших по объему текстов.

Таблица 1

Частотность букв русского алфавита

Символ	P(i)	Символ	P(i)	Символ	P(i)	Символ	P(i)
Пробел	0,175	Р	0,040	Ы	0,016	Ж	0,007
О	0,090	В	0,038	З	0,016	Ю	0,006
Е	0,072	Л	0,035	Ь	0,014	Ш	0,006
Ё	0,072	К	0,028	Ъ	0,014	Ц	0,004
А	0,062	М	0,026	Б	0,014	Щ	0,003
И	0,062	Д	0,025	Г	0,012	Э	0,003
Т	0,053	П	0,023	Ч	0,012	Ф	0,002
Н	0,053	У	0,021	Й	0,010
С	0,045	Я	0,018	Х	0,009

Воспользуемся для подсчета Н формулой (2)

Н»4,72 бит.

Полученное значение Н меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1), является максимальным количеством информации, которое могло бы приходиться на один знак.

Аналогичные подсчеты Н можно провести и для других языков, например, использующих латинский алфавит, английского, немецкого, французского и др. (26 различных букв и «пробел»). По формуле (1) получим

H =log₂27»4,76 бит.

Как и в случае русского знака, частота появления тех или иных знаков неодинакова. Если вести подсчет по формуле (2), то полученное значение будет меньше вычисленного по формуле (1).

Приведем в качестве примера еще одну задачу. В ящике находятся 4 белых и 2 черных шара. Какое количество информации в сообщении, что вытащили белый шар? Какое количество информации в сообщении, что вытащили черный шар? Понятно, что вероятность вытащить белый шар выше, чем вероятность вытащить черный шар. Общее количество возможных событий 4+2=6. Вероятность вытащить белый шар P_бел=4/6=2/3, а вероятность вытащить черный шар Р_чер=2/6=1/3. Общая сумма вероятностей всегда должна быть равна 1. Воспользуемся для подсчета формулой (2):

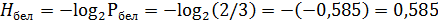бит.

бит.

Объемный (технический) подход

Объемный способ является самым простым способом измерения информации. Объем информации – это количество символов в сообщении. Поскольку, например, одно и то же число может записано многими разными способами (с использованием разных алфавитов), этот способ чувствителен к форме представления сообщения.

В вычислительной технике вся обрабатываемая и хранимая информация вне зависимости от ее природы (число, текст, изображение) представляется в двоичной форме, то есть с использованием алфавита, состоящего всего из двух символов (цифр) 0 и 1. В двоичной системе счисления знаки 0 и 1 называют битами (от английского выражения BInary DigiTs двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления, потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояниях.

Объем информации, записанной двоичными знаками (цифрами) в памяти компьютера или на внешнем носителе информации, подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом невозможно нецелое число битов (в отличие от вероятностного подхода).

Таким образом, количество информации в сообщении определяется по формуле

I = k * H, (3)

где k – количество символов в сообщении,

Н – количество информации в битах, содержащееся в одном символе любого языка (подсчитывается по формуле Хартли).

Для измерения больших объемов информации были введены более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми бит содержит один байт информации. Именно один байт требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2⁸).

Широко используются также ещё более крупные единицы информации:

1 килобайт (Кбайт) = 1024 байт;

1 мегабайт (Мбайт) = 1024 килобайт;

1 гигабайт (Гбайт) = 1024 мегабайт;

1 терабайт (Мбайт) = 1024 гигабайт;

1 петабайт (Пбайт) = 1024 терабайт.

Рассмотрим пример. В сообщении, записанном на языке, алфавит которого состоит из 32 символов, содержится 80 символов. Какое количество информации в байтах содержит данное сообщение? Количество символов в алфавите N =32. По формуле Хартли количество информации, содержащее в одном символе, Н =log₂32=5 бит. Количество информации в сообщении I = k * H =80*5=400 бит =400:8 байт =50 байт.

Приведем в качестве примера еще одну задачу. Необходимо определить, какой объем информации содержит реферат, набранный на компьютере и содержащий 88 страниц, если на каждой странице 50 строк, а в каждой строке – в среднем 60 символов.

Для представления текстов в компьютере используется алфавит из 256 символов. Один символ такого алфавита несет Н =log₂256=8 бит или 1 байт информации. Значит, одна страница будет содержать 50×60=3000 байт информации. Объем все информации в реферате:

3000×88=264000 байт,

264000:1024 Кбайт =257,87125 Кбайт,

257,87125:1024 Мбайт =0,2518 Мбайт.

Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в вероятностном смысле, но заведомо допускает его измерение в объемном смысле. Если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом вероятностное измерение информации не может быть больше объемного.

Дата добавления: 2015-05-10