Элементы теории

Механическая колебательная система с одним резонансом, например в виде пружинного маятника с жесткостью пружины k, массой М и коэффициентом затухания 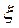при статических нагрузках подчиняется уравнению упругого сжатия F_нагр =k*x.

Тогда статический коэффициент преобразования (или реакции пружинного маятника на статическую нагрузку) будет равен k=x / F_нагр .

Уравнение свободных колебаний такой системы будет иметь следующий вид:

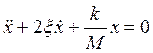
где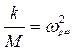

;

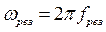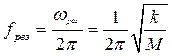
Амплитудно-фазовая частотная характеристика (АФЧХ) колебательной механической системы с одним резонансом:

,

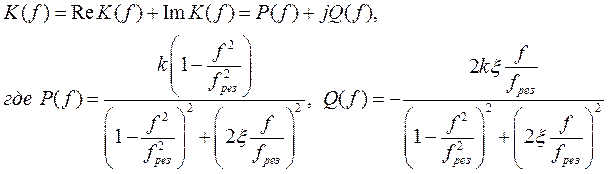где k – коэффициент передачи нагрузки при статическом воздействии, а 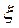- коэффициент затухания.

Если 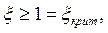то тогда резонанс колебательной механической системы вырождается в апериодическое звено второго порядка. То есть, например при ударе, колебаний не будет, а механическая колебательная система плавно вернется в исходное состояние.

Амплитудная частотная характеристика (АЧХ) колебательного звена:

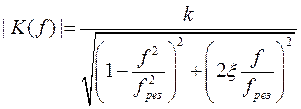
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) колебательного звена

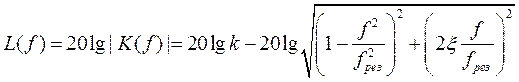
Фазовая частотная характеристика (ФЧХ) колебательного звена

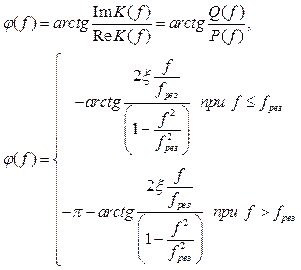
Величина обратная коэффициенту затухания 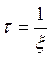называется постоянной затухания, которая равна времени затухания свободных резонансных колебаний, в течении которого амплитуда колебаний уменьшается в е»2,72 раз.

На практике часто используют вместо коэффициента затухания 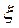, нормированный (по периоду резонанса Т_рез) коэффициент затухания, который называется декрементом затухания и равен .

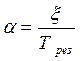В паспортах динамических характеристик зданий и сооружений требуется указывать полученное экспериментальным путем значение логарифмического декремента затухания, который равен

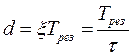
Величина обратная логарифмическому декременту затухания 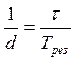равна числу циклов колебаний, совершаемых механической колебательной системой за время, равное постоянной затухания .

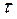Для построения эталонных графиков АЧХ и ФЧХ, которые в естественном виде имеют в качестве координат, прямое отражение для АЧХ зависимости модуля | K | от частоты f, а для ФЧХ зависимость угла фазы 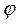в радианах от частоты f, часто используют нормированную систему координат.

В этом случае АЧХ строят в виде зависимости нормированного по k модуля | K |, то есть зависимость от нормированной частоты 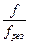, а ФЧХ в виде зависимости 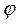от нормированной частоты .

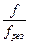Построение графиков экспериментально полученных АЧХ и ФЧХ в нормированных координатах позволяет удобно выполнять графические вычисления коэффициентов затухания реальных механических колебательных систем методом сопоставления с номограммой семейства расчетных АЧХ с разными коэффициентами затухания, построенной также в нормированной системе координат. Для этого экспериментальные АЧХ и ФЧХ строятся в том же масштабе, что и эталонные расчетные номограммы.

Дата добавления: 2015-05-10