Учебный год

Контрольная работа по аналитической геометрии

Оцените ситуацию.

[1] Обзор судебной практики Верховного Суда РФ за третий квартал 2003 г. (по гражданским делам) (утв. постановлениями Президиума Верховного Суда РФ от 3 и 24 декабря 2003 г.) // БВС РФ. 2004. № 3.

для студентов 1 курса ОЗО

Составитель: доц. И.А. Бреус

Вариант 1

1. Написать формулы осевой симметрии плоскости по координатам двух симметричных точек: А(1,-2), В(3,4).
2. Два квадрата имеют общий центр, а их стороны соответственно параллельны. Какими гомотетиями можно один из квадратов отобразить на другой? Постройте.
3. Выяснить, являются ли данные формулы задающими движение:

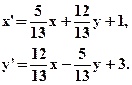
1. Указать вид движения и найти элементы, его определяющие:

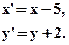
1. На биссектрисе внешнего угла C треугольника АВС взята точка М. Доказать, что |AC|+|CB|£|AM|+|MB|.
2. Составить формулы осевой симметрии, при которой точки (1;-1) и (0;2) являются соответствующими.
3. Доказать, что если прямая, соединяющая середины оснований трапеции, перпендикулярна основаниям, то трапеция равнобочная.

Вариант 2

1. Написать формулы преобразования осевой симметрии, если ось задана уравнением y=kx+b.
2. Стороны одного четырехугольника параллельны сторонам другого, а диагонали первого – диагоналям второго. Следует ли отсюда, что четырехугольники гомотетичны?
3. Выяснить, являются ли данные формулы задающими движение:

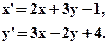
1. Указать вид движения и найти элементы, его определяющие:

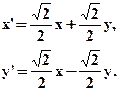
1. В параллелограмм ABCD вписан параллелограмм MNPQ так, что каждой стороне параллелограмма принадлежит по одной вершине другого параллелограмма. Доказать, что центры параллелограммов совпадают.
2. Составить формулы осевой симметрии, при которой точка (-2;-3) является образом точки (4;3).
3. ABCD – равнобочная трапеция с основаниями АВ и CD. Р и Q – точки пересечения медиан треугольников АВС и ADB. Доказать, что |PD|=|QC|.

Вариант 3

1. Доказать, что точки, симметричные точке М относительно середин сторон данного четырехугольника, являются вершинами параллелограмма.
2. Доказать, что если центр гомотетии О гомотетичных треугольников ABC и A’B’C’ совпадает с центром тяжести одного треугольника, то он является центром тяжести другого.
3. Выяснить, являются ли данные формулы задающими движение:

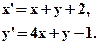
1. Указать вид движения и найти элементы, его определяющие:

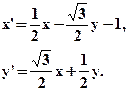
1. На боковых сторонах АС и ВС равнобедренного треугольника АВС даны точки M и N так, что |CM|+|CN|=|AC|. Доказать, что отрезок, соединяющий середины боковых сторон проходит через середину отрезка MN.
2. Составить формулы осевой симметрии, зная уравнение оси в следующем случае: 2х-3у=0.
3. Доказать, что сумма расстояний от любой точки основания равнобедренного треугольника до боковых сторон постоянна.

Вариант 4

1. На сторонах параллелограмма ABCD вне его построены правильные треугольники ABM, BCN, CDP, DAQ. Доказать, что точки M, N, P, Q являются вершинами параллелограмма.
2. Доказать, что одна из двух неравных окружностей может быть переведена в другую двумя различными гомотетиями, причем сумма коэффициентов этих гомотетий равна нулю.
3. Выяснить, являются ли данные формулы задающими движение:

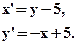
1. Указать вид движения и найти элементы, его определяющие:

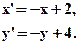
1. Даны две равные окружности (O1,r) и (O2,r), пересекающиеся в точках M и N. Прямая l, параллельная прямой O1O2, пересекает окружность (O1,r) в точках А и В, а окружность (O2,r) в точках С и D. (Лучи АВ и СD сонаправлены). Доказать, что величина угла АМС не зависит от положения прямой l.
2. Составить формулы осевой симметрии, зная уравнение оси в следующем случае: х+2у-3=0.
3. Доказать, что прямая, соединяющая точку пересечения диагоналей равнобочной трапеции с точкой пересечения продолжений боковых сторон, перпендикулярна основаниям трапеции и делит их пополам.

Вариант 5

1. Поворот вокруг точки М(2;1) отображает точку А на точку В. Найти координаты точки В, если a=45°, А(1;-2).
2. Две окружности пересекаются в точках А и В. Доказать, что если M и N центры гомотетий этих окружностей, то ÐMAN=ÐMBN=90°.
3. Выяснить, являются ли данные формулы задающими движение:

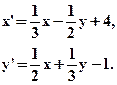
1. Указать вид движения и найти элементы, его определяющие:

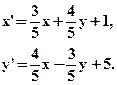
1. На сторонах произвольного треугольника АВС вне его построены правильные треугольники АВС1, ВСА1, САВ1. Доказать, что отрезки АА1, ВВ1, СС1 равны.
2. Составить формулы осевой симметрии, зная уравнение оси в следующем случае: 3х+1=0.
3. Окружность, центр которой принадлежит биссектрисе угла АВС, пересекает стороны этого угла соответственно в точках M и N, P и Q. Доказать, что |MN|=|PQ|.

Вариант 6

1. Поворот вокруг точки М(2;1) отображает точку А на точку В. Найти координаты точки В, если a=120°, А(1;1).
2. Доказать, что если в треугольниках АВС и А’В’С’ выполняются равенства: |A’B’|=k|AB|, |A’C’|=k|AC|, ÐBAC=ÐB’A’C’, то эти треугольники подобны.
3. Выяснить, являются ли данные формулы задающими движение:

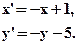
1. Указать вид движения и найти элементы, его определяющие:

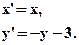
1. Найти координаты образа точки (Ö3;1) при движении с единственной инвариантной точкой (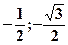), зная, что точка (0;0) переходит в точку (-1;0).
2. Найти уравнение образа окружности 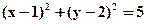при переносе, для которого прямые 2х+3у=0 и х+у=0 являются соответственно прообразами прямых 2х+3у-2=0 и х+у+1=0.
3. Даны три точки А, В, С, не лежащие на одной прямой. Доказать, что оси симметрии каждых двух точек, взятых попарно, пересекаются в одной точке.

Вариант 7

1. Поворот вокруг точки М(2;1) отображает точку А на точку В. Найти координаты точки В, если a=90°, А(3;-1).
2. Доказать, что если в треугольниках АВС и А’В’С’ выполняются равенства: |A’B’|=k|AB|, |A’C’|=k|AC|, |AB|=k|A’B’|, то эти треугольники подобны.
3. Для данного движения найти образы и прообразы точек

М(0;0) и Р(2;-1):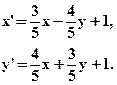

1. Указать вид движения и найти элементы, его определяющие:

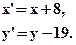
1. Пусть А(2;5) и В(-1;-1) – инвариантные точки движения, отличные от тождественного преобразования. Найти уравнение образа окружности 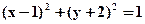при этом движении.
2. Найти уравнение прообраза прямой 5х-7у+9=0 при переносе, для которого прямая х-2у=0 инвариантна, а прямая 3х-4у=0 переходит в прямую 3х-4у+2=0.
3. Треугольник АВС переходит при переносе в треугольник A’B’C’. Доказать, что соответствующие медианы этих треугольников параллельны.

Вариант 8

1. Даны точка М(5;1) пересечения медиан равностороннего треугольника АВС и уравнение прямой АВ: 2х-у=0. Написать уравнения прямых АС и ВС.
2. Доказать, что если в треугольниках АВС и А’В’С’ выполняются равенства: ÐABC=ÐA’B’C’, ÐBCA=ÐB’C’A’, то эти треугольники подобны.
3. Для данного движения найти образы и прообразы точек

М(0;0) и Р(2;-1):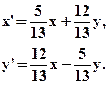

1. Указать вид движения и найти элементы, его определяющие:

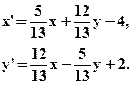
1. Найти уравнение прообраза прямой у=0 при движении с единственной инвариантной прямой 2х-4у+9=0, зная, что точка (2;1) переходит в точку (3;6).
2. Найти координаты прообраза точи (6;-8) при переносе, зная, что точка (2;-5) является прообразом точки (-3;2).
3. На сторонах АВ и CD параллелограмма ABCD построены квадраты: первый – вне параллелограмма, а второй – по ту же сторону от прямой CD, что и сам параллелограмм. Доказать, что расстояние между центрами квадратов равно |ВС|.

Вариант 9

1. Через центр правильного треугольника проведены две прямые, угол между которыми равен 60°. Доказать, что пересечение этих прямых с данным треугольником представляет собой два равных отрезка.
2. В данной прямоугольной декартовой системе координат записать координатное задание гомотетии с центром С(-2;1) и коэффициентом k=3.
3. Для данного движения найти образы и прообразы точек

М(0;0) и Р(2;-1):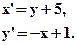

1. Найти уравнения инвариантных прямых движения

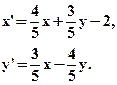
1. Определить вид движения, переводящего точки А(1;-1), В(2;1), С(-1;-2) соответственно в точки A’(0;9), B’(2;10), C’(-1;7) и составить его формулы.
2. Найти координаты прообраза точки (3;-1) при переносе, для которого прямая 3х+4у-7=0 инвариантна, а расстояние между соответствующими точками равно 15.
3. На сторонах правильного треугольника, вне его, построены квадраты. Доказать, что центры квадратов являются вершинами правильного треугольника.

Вариант 10

1. Доказать, что точки, симметричные точке М пересечения высот треугольника относительно прямых, содержащих его стороны, лежат на окружности, описанной около этого треугольника.
2. В репере R даны координаты точек А(2;1), В(3;-2), С(1;0), A’(-1;-5), B’(-3;1), C’(1;-3). Доказать, что треугольники DABC и DA’B’C’ гомотетичны и написать формулы гомотетии h: DABC ® DA’B’C’.
3. Для данного движения найти образы и прообразы точек

М(0;0) и Р(2;-1):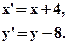

1. Найти уравнения инвариантных прямых движения

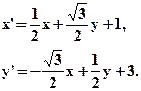
1. Составить формулы движения первого рода, при котором прямая 2х+у+1=0 является образом прямой 2х+у-1=0, а точка А(1;-2) – инвариантна.
2. Найти координаты образа точи (-1;2) при переносе, зная, что точка (0;4) переходит в точку (-3;7).
3. Дан квадрат ABCD и точки 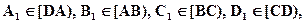такие, что 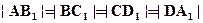. Доказать, что 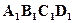- квадрат.

Дата добавления: 2015-05-10