Метод Ньютона с использованием аналитического представления функции

Метод половинного деления

e = 1e-04; %Устанавливаем допустимую погрешность

dx = 0.1; %шаг х при поиске интервала, содержащего корень

a = -1;

b = a;

while fun(a)*fun(b) > 0 %Определяем интервал, на котором

b = b + dx; % функция F(x) меняет знак

end;

a = b - dx;

x = (a+b)/2; % Первое приближение корня -

% середина найденного интервала

I = 1; % Счетчик итераций устанавливаем в "1"

X=[x]; % Формирование массивов для графиков

Y=[fun(x)];

while abs(fun(x)) > e

if fun(x) * fun(a) < 0 %Если функция имеет разные знаки

%на концах отрезка,

b = x; %сдвигаем правую границу

else

a = x; % иначе сдвигаем левую границу

end;

x = (a+b)/2; %и вычисляем следующее приближение

I = I + 1; %увеличиваем количество итераций на 1

X = [X x];

Y = [Y fun(x)];

end;

Str = ['Значение корня: ' num2str(x) '; Количество итераций: ' num2str(I)];

disp(Str)

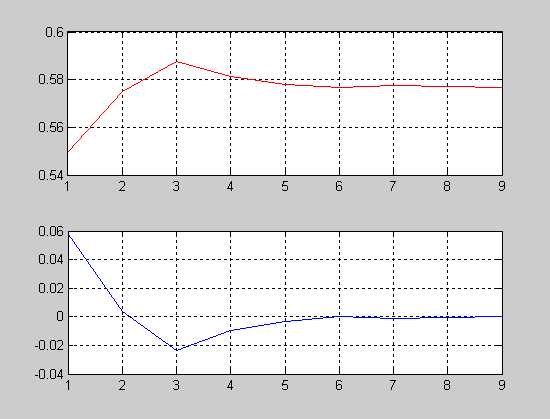
figure %Построение двух графиков в одном графическом окне

subplot(2, 1, 1);

plot(X, '-r'), grid on

subplot(2, 1, 2);

plot(Y, '-b'), grid on

x0=0.5;

x=fzero('fun', x0) % проверка

syms x; % cимвольная (аналитическая) переменная

% определяется аналитическое описание функции F(x)

f = (1 - x)^(1/2) - tan(x);

f1 = diff(f); % определяется производная функции F'(x)

ezplot(f), grid on % строится график функции для визуального

% определения первого приближения корня.

x0 = input('Задайте значение x0: ') % вводом с клавиатуры

% задается первое приближение корня

err = 1e-05; % задается допустимая погрешность вычисления корня

delta = x0; % текущая погрешность вначале равна допустимой погрешности

X = [ x0 ]; % формируется вектор последовательных приближений

% корня к его конечному значению

n = 1; % номер первого приближения

N = [ n ]; % формируется вектор номеров приближений корня

% организуется цикл определения последовательных приближений корня

% методом Ньютона

while abs(delta) > err % повторять вычисления пока текущая погрешность

% больше допустимой

x1 = x0 - subs(f, x, x0) / subs(f1, x, x0); % Вычисляется следующее

% приближение корня.

delta = x1 - x0; % вычисляется текущая погрешность вычислений

x0 = x1; % следующее приближение становится текущим

X = [X x1]; % в вектор Х добавляется следующее приближение

n = n+1; % номер следующего приближения

N = [N n]; % в вектор N добавляется номер следующего приближения

end;

str_out = 'x = '; % формируется строка вывода результатов вычисления корня

res = num2str(x1);

str_out = strcat(str_out, ' ', res);

disp(str_out); % строка вывода отображается в командном окне

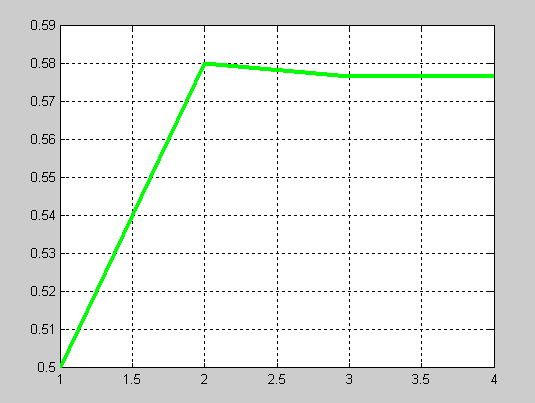
plot(N, X, 'Linewidth', 3, 'Color', [0 1 0]), grid on % строится график

% приближения корня

Задание №2.

Дата добавления: 2015-05-10