Содержательный подход к измерению количества информации

Теоретические сведения

Порядок выполнения работы

Лабораторная работа №9

Тема: «Измерение информации»

Цель работы: познакомиться с основными подходами к измерению информации и использовать их при решении задач.

1. Познакомиться с системой единиц измерения количества информации.

2. Рассмотреть содержательный и алфавитный подходы к измерению информации.

3. Закрепить полученные навыки при решении задач.

Минимальную порциюинформации о каком-либо свойстве объекта принято называть битом (binary digit – двоичная цифра). Бит – единица измерения информации, представляющая собой выбор из двух равновозможных вариантов. Бит представляет собой обозначение одного двоичного разряда, способного, в зависимости от сделанного выбора, принимать значение 1 или 0.

Байт – единица измерения информации, представляющая собой последовательность состоящую из 8 бит.

1 байт = 2³ бит = 8 бит.

Каждый бит имеет определенное место внутри байта, которое называется разрядом. Разряды принято нумеровать справа налево. Например, третий бит в байте на самом деле находится в пятом разряде байта.

Для измерения больших объемов информации принято использовать производные единицы измерения, представленные в таблице:

Название	Степень	Условное обозначение
Килобайт	2^10 (1024 байт)	Кбайт, KB
Мегабайт	2^20 (1024 Кбайт)	Мбайт, MB
Гигабайт	2^30(1024 Мбайт)	Гбайт, GB
Терабайт	2^40 (1024 Гбайт)	Тбайт, TB
Петабайт	2^50 (1024 Тбайт)	Пбайт, PB
Эксабайт	2^60 (1024 Пбайт)	Эбайт, EB
Зеттабайт	2^70 (1024 Эбайт)	Збайт, ZB
Йоттабайт	2^80 (1024 Збайт)	Йбайт, YB

Задание №1

Заполнить пропуски значениями, в соответствии с предложенными единицами измерения:

№ варианта	Условие
	5 Кбайт = _? _ байт = _? _ бит; 512 Кбайт = 2^? байт = 2^? бит.
	_? _ Кбайт = _? _ байт = 12288 бит; 256 Гбайт = 2^? Мбайт = 2^? Кбайт.
	_? _ Гбайт = 1536 Мбайт = _? _Кбайт; 256 Кбайт = 2^? байт = 2^? бит.
	_? _ Гбайт = _? _ Мбайт = 2500 байт; 512 Мбайт = 2^? Кбайт = 2^? байт.
	_? _ Кбайт = _? _ байт = 213 бит; 0,5 Кбайт = 2^? Кбайт = 2^? байт.
	2 Гбайт = _? _ Мбайт = _? _ Кбайт; 256 Мбайт = 2^? Кбайт = 2^? байт.
	5 Мбайт = _? _ Кбайт = _? _ байт; 768 Кбайт = 2^? байт = 2^? бит.
	_? _ Кбайт = _? _ байт = 1073741 бит; 768 Мбайт = 2^? Кбайт = 2^? байт.
	_? _ Гбайт = 15 Мбайт = _? _Кбайт; 0,5 Мбайт = 2^? байт = 2^? бит.
	_? _ Гбайт = _? _ Мбайт = 1073741824 байт; 512 Гбайт = 2^? Мбайт = 2^? Кбайт.
	_? _ Кбайт = _? _ байт = 1024 бит; 768 Гбайт = 2^? Мбайт = 2^? Кбайт.
	1,5 Гбайт = _? _ Мбайт = _? _ Кбайт; 0,5 Гбайт = 2^? Кбайт = 2^? байт.

Новые сведения о свойствах объектов окружающего нас мира содержат информацию для человека и, следовательно, пополняют его знания. При содержательном подходе возможна качественная оценка полученной информации, например, насколько она для нас полезна, важна или наоборот – вредна.

Неопределенность знания о некотором событии – это количество возможных результатов события (бросания монеты, кубика; вытаскивания жребия и пр.). Уменьшение неопределенности знания человека в 2 раза, несет для него 1 бит информации.

Количество информации (I) для событий с различными вероятностями определяется по формуле К.Шеннона:

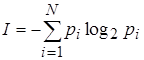
где N — количество возможных событий; 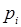— вероятности отдельных событий.

Если события равновероятны, то количество информации (I) определяется по формуле Р.Харт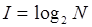ли:

или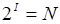

где N – количество равновероятных событий.

Пример 1.

После экзамена по информатике объявляют оценки («5», «4», «3» или «2»). Какое количество информации будет нести сообщение об оценке студента А, который выучил лишь половину билетов, и сообщение об оценке учащегося Б, который выучил все билеты.

Решение. Опыт показывает, что для учащегося А все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке, можно вычислить по формуле Хартли:

I = Iog ₂ 4 = 2 бита.

На основании опыта также предположим, что для студента В наиболее вероятной оценкой является «5» (р₁ = 1/2), вероятность оценки «4» в два раза меньше (р₂ = 1/4), а вероятности оценок «2» и «3» еще в два раза меньше (р₃ = p₄ =1/8). Так как данные события не являются равновероятными, для подсчета количества информации воспользуемся формулой Шеннона:

I = - ( 1/2·log₂l/2+1/4·log₂l/4+1/8·log₂l/8+1/8·log₂l/8)бит= 1,75 бит

(log₂l/2=-1, log₂l/4=-2, log₂l/8=-3)

Пример 2.

В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение том, что выпал номер 17?

Решение. Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения: 2 ^I =32. Так как 32=2⁵, то I =5 бит. (Ответ не зависит от того, какой именно выпал номер).

Задание №2

№ варианта	Условие задачи
	Какое количество информации несет в себе сообщение о том, что нужный вам файл находится на одном из восьми дисков?
	В рулетке общее количество лунок равно 128. Какое количество информации вы получите в сообщении об остановке шарика в одной из лунок.
	Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8 после первого хода первого игрока, играющего «крестиками»?
	Сообщение о том, что ваш друг живет на десятом этаже, несет в себе 4 бита информации. Сколько этажей в доме?
	Какое количество информации получит второй игрок при игре в крестики-нолики на поле 4х4 после первого хода первого игрока?
	При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит данный диапазон?
	Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?
	Группа студентов пришла в бассейн, в котором 4 дорожки для плавания. Инструктор сообщил, что группа будет плавать на дорожке №3. Сколько информации получили студенты из этого сообщения?
	В корзине лежат 8 шаров разного цвета. Сколько информации несет сообщение о том, что из корзины достали зеленый шар?
	Было получено сообщение «Встречайте! Вагон №7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
	Сообщение о том, что ваш друг живет на десятом этаже несет в себе 5 бит информации. Сколько этажей в доме?
	При угадывании целого числа в некотором диапазоне было получено 7 бит информации. Сколько чисел содержит данный диапазон?

Дата добавления: 2015-05-10