Момент силы относительно оси

Момент силы относительно точки

Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.

Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452--1519).

Моментом силы относительно точки называется произведение модуля силы на ее плечо:

М0(?) = РИ.

Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.

Единица момента силы:

[М] = [У7] [/; ] = сила х длина = ньютон х метр = Н * м.

Условимся считать момент силы положительным, если сила стремится вращать свое плечо вокруг центра момента против часовой стрелки, и наоборот (рис. 3.4).

Одна и та же сила относительно разных точек может давать и положительный и отрицательный момент.

Момент силы относительно точки, лежащей на линии действия этой силы, равен нулю, так как в этом случае плечо равно нулю.

Момент силы относительно точки не меняется при перенесении силы вдоль линии ее действия, так как модуль силы и плечо остаются неизменными.

Лемма о проекциях позволяет ввести в рассмотрение новую характеристику силы по отношению к оси. Определение. Моментом силы F относительно оси z называется алгебраическая величина, равная проекции на эту ось момента силы относительно произвольной точки указанной оси.

m_z(F)=пр_z m_A(F) (A принадлежит z) (17)

Рассмотрим способ вычисления и свойства момента. Пользуясь произволом выбора центра моментов на оси, выберем в качестве такового т.О- проекцию точки А приложения силы на ось z. Обозначив через к орт оси z, и применив круговую перестановку в смешанном произведении, запишем

m_z(F)= k.(OAxF)=(kxOA).F=hFCosa (18)

Здесь учтено, что ввиду взаимной перпендикулярности векторов k и OA, модуль произведения kxOA равен расстоянию ОА точки приложения сил до оси.

Формула показывает, что:

а) Момент относительно оси дает только составляющая силы, направленная по касательной t к окружности радиуса h.

. Из Рис.8 вытекаетaб) Знак момента определяется знаком Cos

Рис.8 следующее правило знаков: ^ Момент силы относительно оси положителен, если с конца оси видно, что сила стремится повернуть тело против часовой стрелки.

/2). Это происходит, когдаpИз формулы (12) вытекает, что момент силы относительно оси равен нулю в cлучае, если сила и ось лежат в одной плоскости (a=

1.
сила параллельна оси

2.
линия действия силы пересекает ось

^

Выберем систему координат Oxyz. Вектор можно построить, зная модуль и углы 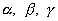между вектором и соответствующими осями (рис. 14 ).

Задание этих величин и определяет силу . Точка приложения силы должна быть задана дополнительно координатами х, у, z. Кроме того, силу можно задавать проекциями на оси . Тогда

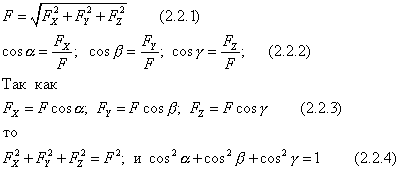
Эти формулы позволяют, зная проекции силы на оси координат найти ее модуль и углы с осями, т.е. определить силу. Зная проекции, можно построить вектор геометрически.

Для плоскости формулы (2.2.1) и (2.2.2) запишутся

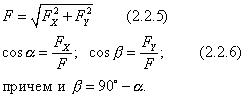
Построение в плоскости производится по 4-й аксиоме статики.

Рассмотрим теперь аналитический способ сложения сил. Зависимость между векторами и их проекциями дает следующая теорема:

Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось (рис. 15 ).

Дата добавления: 2015-05-10