Закон умножения вероятностей зависимых событий

Закон умножения вероятностей независимых событий

Закон сложения вероятностей независимых событий

В том случае, если интересующее событие А объединяет группу или сумму событий A1, A2, A3 и т. д., то вероятность появления этого события А или вероятность суммы событий A1 + A2 + A3 и т. д. равно сумме вероятностей этих событий P (A₁ + A₂ + A₃) = P (A₁) + P (A₂) + P (A₃).

Вероятность совместного проявления двух и более независимых событий А, Б и т. д. в полной группе событий равно произведению вероятностей этих

событий P(А,Б) = P(А)∙ P(Б).

Вероятность совместного появления двух и более зависимых событий А, Б и т. д. в полной группе событий равна произведению вероятности появления первого события на условную вероятность второго события:

P(A, Б) = P(A)∙P(Б A).

Практическая часть

Исходные данные: Таблица 1

Вариант 6
N	m1	m2	m3	m4	m5

Задание 1

Были проведены испытания N тракторов. При этом установлено, что у m₁ тракторов эксплуатационные отказы появились в интервале наработок A₁ =100…200 мото-ч, у m₂ – в интервале A₂ = 200...300 мото-ч, у m₃ – в интервале A₃ = 300...400 мото-ч, у m₄ – в интервале A₄ = 400...500 мото-ч и, наконец, у m₅ – в интервале A₅ = 500...600 мото-ч.

Требуется определить, чему равна опытная вероятность появления эксплуатационного отказа в каждом интервале наработки трактора.

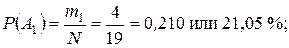
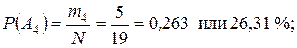
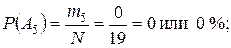
Задание 2

Требуется определить, какой процент тракторов в условиях предыдущего задания будет иметь отказы в интервале их средней наработки от 200 до 500 мото-ч.

Событие А – количество отказов тракторов в интервале наработок от 200 до 500 моточасов определяет три события:

A ₂ – количество отказов в интервале от 200 до 300 мото-ч;

A ₃ – количество отказов в интервале от 300 до 400 мото-ч;

A ₄ – количество отказов в интервале от 400 до 500 мото-ч.

Следовательно, ожидаемое количество отказов в интервале параметров от 200 до 500 мото-ч определим по закону сложения вероятностей независимых событий. P (A) = P (A₂) + P (A₃) + P (A₄)

P (A) =0,210+0,315+0,236=0,761

Задание 3

В двух колхозах работают по N тракторов одной марки, эксплуатационные отказы которых распределены по закону, приведенному в задании 1. Необходимо определить вероятности совместного проявления отказа у трактора A из первого колхоза и у трактора Б из второго колхоза в интервале их наработок A₃ =300...400 мото-ч.

Эти два события не связаны между собой, так как вероятность появления одного из них не зависит от того, произошло или не произошло второе событие. Поэтому применяется уравнение.

P(А(А₃); Б(А₃)) = P(А(А₃)∙ P(Б(А₃))=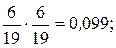

Задание 4

По данным определить вероятность совместного появления отказов у тракторов А и Б, работающих в одном колхозе, при их средней наработке A 3 =300...400 мото-ч.

Эти два события связаны между собой, так как вероятность появления одного из них зависит от того, произошло или нет второе событие (появление отказа у трактора Б). Поэтому вероятность появления одного из них зависит от того, произошло или нет второе событие (появление отказа у трактора Б). Поэтому вероятность совместного появления отказов у тракторов А и Б определяется по закону умножения вероятностей зависимых событий.

P(А(А₃); Б(А₃)) = P(А) ∙ P(Б│А) =

Задание 5

Из условий таблицы 3.1 определить полную группу событий всех возможных вариантов совместного появления отказов у тракторов А и Б, работающих в разных колхозах и при их разных наработках.

1. Определим количество событий в полной группе: трактор А отказал в интервале наработок A₁ = 100...200 мото-ч, а трактор Б соответственно A₁ = 100...200, A₂ = 200...300, A₃ = 300...400, A₄ = 400...500 и A₅ = 500...600 мото-ч, всего 5 событий. Аналогично по 5 событий произойдет при отказе трактора А в интервале A₂ = 200...300, A₃ = 300...400, A₄ = 400...500 и A₅ = 500...600 мото-ч. Таким образом, полная группа событий состоит из 25 отдельных событий.

2. Определим вероятность всех событий в полной группе (события несвязанные):

Задание 6

Для условий задания 1 (табл. 3.1) (N тракторов работают в одном хозяйстве) определить полную группу событий всех возможных вариантов совместного появления отказов у тракторов А и Б при всех возможных вариантах их наработок.

1. Определим количество событий в полной группе рассуждая так же, как в предыдущем задании, определяем, что число событий полной группы равно 25.

2. Определим вероятность всех событий в полной группе (события связанные):

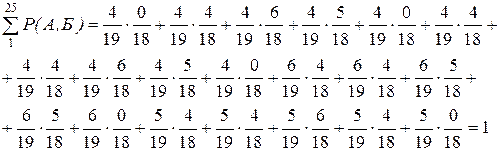
Задание 7

На складе готовой продукции ремонтного предприятия имеется N двигателей, из которых m1 отремонтированных и m2 новых (из обменного фонда) (табл. 3.2). Заказчик получает со склада 2 двигателя. В этом случае полную группу событий образуют следующие четыре события:

1) оба двигателя новые;

2) оба двигателя отремонтированные;

3) первый двигатель отремонтированный, второй – новый;

4) первый двигатель новый, второй – отремонтированный.

Требуется определить:

а) вероятность того, что оба двигателя окажутся новыми;

б) вероятность того, что хотя бы один двигатель из двух окажется новым.

События связанные.

Исходные данные Таблица 2

Вариант	N	m1	m2

Для решения воспользуемся уравнением связанных событий

P(Д_н;Д_н) = P(Д_н) ∙ P(Д_н │ Д_н) =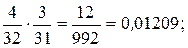

Условиям задачи соответствует 1, 3 и 4-е события. Вероятность появления каждого события определяется по закону умножения зависимых событий, а вероятность получения хотя бы одного нового двигателя по закону сложения вероятностей трех этих событий

P (Д_н из 2Д) = P (Д_н;Д_н)+ P (Д_р;Д_н)+ P (Д_н;Д_р)= P(Д_н) ∙ P(Д_н │ Д_н) +

+ P(Д_р) ∙ P(Д_н │ Д_р) + P(Д_н) ∙ P(Д_р │ Д_н) =

= .

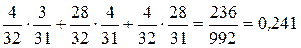Решение этого задания может быть упрощено применением противоположных событий. В данном случае противоположным событием является получение двух отремонтированных двигателей. Вероятность такого события определяется по уравнению

P(Д_р;Д_р) = P(Д_р) ∙ P(Д_р │ Д_р) =

Вероятность получения хотя бы одного нового двигателя из двух определяется по уравнению

P (Д_н из 2Д) = 1− P (Д_р,Д_р)= 1− 0,762 = 0,23.

Правильность решения этого примера может быть проверена по сумме вероятностей полной группы событий, которая должна быть равна единице:

Вывод: в процессе проделанной лабораторной работы, научились определять вероятность появления случайной величины.

Дата добавления: 2015-05-10