УРОК № 20

(алгебра 9 клас)

Тема уроку. Найпростіші перетворення графіків функцій.

Мета уроку: сформувати розуміння учнями змісту поняття «перетво­рення графіка функції», а також розуміння того факту, що певне перетворення рівняння функції тягне за собою перетворення графіка та навпаки. Сформувати знання учнів про основні види геометричних перетворень графіків функцій (на інтуїтивному рівні) та про рівняння функції, що задається цим перетворенням. Сформувати первинні уміння «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), а також виконува­ти побудови графіків функцій за допомогою перетворень, заданих рівнянням даної функції.

Тип уроку: формування знань і первинних умінь.

Наочність та обладнання: опорний конспект № 14, роздавальний матеріал (картки з розв'язаннями домашніх вправ).

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Для економії часу на уроці в разі необхідності вчитель може запропонувати учням роздавальний матеріал — розв'язання до­машніх вправ — самостійно опрацювати вдома.

Для організації поточного контролю за засвоєнням учнями знань та вмінь можна запропонувати їм тестові завдання (див. нижче), перевірка яких проводиться одразу після виконання. Учитель фіксує прізвища тих учнів, які потребують додаткової педагогічної уваги для можливості здійснення певної корекційної роботи.

Тестові завдання

1. На рисунку зображений графік функції, область визначення якої D(f) = R. Правильним є твердження:

а) нулі функції: 2; 2,5; f(x) зростає, якщо х 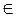[-2; 3]; f(x) < 0, якщо

x 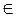(5; +∞);

б) нулі функції: 2; 5; f(x) зростає, якщо x 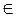[-2; 2]; f(x) < 0, якщо

х 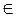[5; +∞);

в) нулі функції:-2; 5; проміжок зростання x 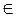[-2; 2]; f(х) < 0, якщо

х 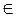(5; +∞);

г) нулі функції: 3; проміжку зростання немає; f(x) < 0, якщо

x 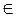(-∞; -2) і x 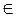(2; + ∞).

2. Область визначення функції у = :

а) х 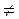5; б) х 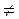-5; в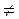) х -5, х 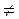0; г) х 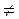3.

3. Область значень функції f(x) = x ² – 3:

а) (-∞; +∞); б) [3; +∞); в) [-3; +∞); г) (-3; +∞).

4. Якщо f(x) = 3 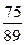х – 1, то:

а) f (3) < f (4); б) f (3) > f (4); в) f (3) < f (4); г) f (3) = f (4).

5. Значення функції у (х) = -3 х + 8 додатні, якщо:

а) х ≤ 2 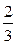; б) х ≥ 2 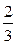; в) х < 2 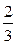; г) таких значень х немає.

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

На цьому етапі уроку доречними будуть слова вчителя про те, що дослідження функцій за готовим графіком є більш простим, ніж за формулою (підтвердженням цієї думки можуть стати результати перевірки тестових завдань). Розвиваючи цю думку, вчитель пові­домляє учням про те, що в ряді випадків для розв'язування задач необхідно буває побудувати графік функції, яка не є елементарною (учитель може навести ряд прикладів таких функцій). Отже, фор­мулюється питання: чи існують засоби (і якщо існують, то як ними користуватися), за допомогою яких можна побудувати графік дея­кої функції, використовуючи при цьому вміння будувати графіки елементарних функцій (лінійної, оберненої пропорційності, ква­дратичної функції та функції у = 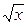). Зрозуміло, що пошук відпо­віді на поставлене питання і є основною дидактичною метою уроку.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Яка з наведених функцій є зростаючою:

а) на області визначення; б) на проміжках (-∞; 0) і (0; +∞)?

1) у = 4 х – 1;2) у = 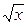; 3) у = - 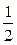x + 1; 4) у = 3 х;

5) у = ; 6) у = х ²; 7) у = - .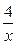

2. Графіком якої з наведених функцій є пряма, що проходить через початок координат? Поясніть свою відповідь, не вико­нуючи побудови:

1) у = 2 х + 1; 2) у = 2 х; 3) у = 2 х ²; 4) у = 2; 5) у = 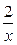; 6) у = .

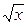3. На одному з рисунків зображено графік функції у = 2 х. Ука­жіть цей рисунок.

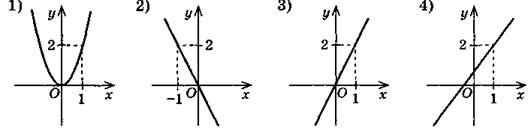
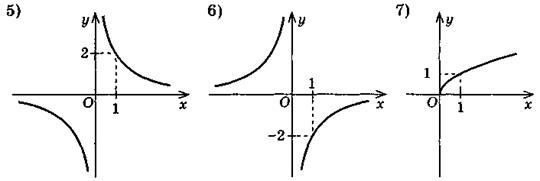
4. Для функції f(x) = x ² – 3 знайдіть значення виразу:
1) f (-2); 2) f (-1); 3) f (0); 4) f (1); 5) f (2); 6) f (3);

7) f (4); 8) f (5); 9) f (6).

Дата добавления: 2015-05-10