V. Формування знань

План вивчення нового матеріалу

1. Уявлення про перетворення графіка функції.

2. Побудова графіків паралельним перенесенням вздовж осі ор­динат (абсцис).

3. Побудова графіка функції симетрією відносно осі абсцис.

4. Розтягнення (стиснення) графіка функції вздовж осі ординат.

Опорний конспект №14

	Найпростіші перетворення графіків функцій
	№ з/п	Формула залежності	Приклад	Перетворення
		y = - f(х)		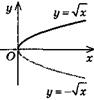Симетрія відносно осі Ох
		y = f(х) + a		Паралельне перене­сення вздовж осі Оу на а одиниць (якщо а > 0, то вгору, якщо а < 0, то вниз)
		y = f(х + a)		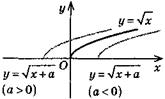Паралельне перене­сення вздовж осі Ох на + а одиниць (якщо а > 0 — вліво, якщо а < 0 — вправо)
		y = kf(х) (k > 0 )		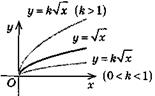Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k > 1, і стиснуто, якщо 0 < k < 1

Методичний коментар

Одразу слід зауважити, що вивчення питання про геометричні перетворення графіків функцій на даному уроці є досить складним через певну невідповідність програм вивчення геометрії та алге­бри у 9 класі. Ця невідповідність існувала у попередньо діючій програмі і, на жаль, збереглася в програмі для 12-річної школи. Тому формування уявлення про геометричні перетворення графі­ків функцій проводиться на даному уроці на інтуїтивному рівні, і вчителеві не слід акцентувати увагу на строгих означеннях ви­ділених ним видів перетворень. Основна увага приділяється, вста­новленню і засвоєнню учнями зв'язку між рівнянням функції та певним видом перетворення графіка функції (цей зв'язок відобра­жено в опорному конспекті № 14). Вивчення зв'язку між видом пе­ретворення та рівнянням функції, як це відбувалось останні роки, проводиться через обчислення значень функції в окремих точках і спостереження за зміною значень функції в цих точках залежно від зміни виду функції. Результати даних «спостережень» мають вигляд таблиці (див. опорний конспект № 14).

VI. Формування вмінь

Усні вправи

1. Як треба перетворити графік функції y = f(x), щоб утворився графік функції:

1) y = -f(x); 2) y = f(x + 2 ); 3) y = f(x – 2 ); 4) y = f(x) + 2;

5) y = f(x) – 2; 6) y = 2 f(x); 7) y = ?

2. Дано графіки функцій:

a) y = xa; б) y = 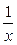; в) у = .

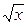Яке рівняння буде мати функція, графік якої утвориться із да­них графіків функцій: 1) при паралельному перенесенні вгору на 3 одиниці; 2) при розтягненні в 3 рази; 3) при паралельному перенесенні вправо на 3 одиниці?

Письмові вправи

Зміст вправ, запропонованих до розв'язування на уроці, може бути таким:

1) серед заданих графіків функцій вибрати ті, що відповідають даним рівнянням;

2) побудувати графік функції, що задана рівнянням, виконавши відповідне до рівняння геометричне перетворення;

3) на повторення: дослідити функцію, задану графічно, на моно­тонність, знайти її нулі, проміжки зростання й спадання та область значень.

(Завдання на побудову графіків функцій шляхом геометрич­них перетворень на даному уроці мають початковий або середній рівень складності.)

Методичний коментар

Формуванню сталих умінь виконувати побудову графіків функцій шляхом перетворень графіків елементарних функцій має передувати робота з повторення питань про види та особливості графіків елементарних функцій (ця робота проводилась протягом останніх чотирьох уроків). Формування вмінь виконувати побу­дову графіка функції шляхом геометричних перетворень ведеться паралельно із закріпленням знань учнів про формули, що відпо­відають цим перетворенням. Тому при виконанні як усних, так і письмових вправ на цьому та наступному уроках вчителеві слід вимагати від учнів в першу чергу аналізу формули даної функції, а потім вже вибору відповідно до неї геометричного перетворення, для побудови графіка функції. Такий підхід, по-перше, сприяє швидшому засвоєнню учнями змісту навчального матеріалу уро­ку, а по-друге, допомагає попередити помилки, які часто виника­ють в учнів, особливо, коли мова йде про паралельне перенесення вздовж різних координатних осей.

VII. Підсумки уроку

Дата добавления: 2015-05-10