Розділ 2. Випадкові величини

Випадкова величина – величина, яка в результаті експерименту (випробування) набуває одного з можливих значень з певною ймовірністю.

Дискретна випадкова величина – випадкова величина, множина можливих значень якої є скінченна або зліченна.

Закон розподілу дискретної випадкової величини – відповідність між її можливими значеннями та їх ймовірностями.

Математичне сподівання дискретної випадкової величини – сума добутків усіх її можливих значень на їх ймовірності.

Відхилення дискретної випадкової величини від її математичного сподівання – різниця між цією величиною та її математичним сподіванням.

Дисперсія дискретної випадкової величини – математичне сподівання квадрата відхилення цієї величини від її математичного сподівання.

Неперервна випадкова величина – випадкова величина, можливі значення якої заповняють деякий інтервал, або випадкова величина, функція розподілу якої неперервна і кусково диференційовна.

Функція розподілу випадкової величини (дискретної або неперервної) – імовірність того, що випадкова величина набуде значення, меншого за число х.

Густина (щільність) розподілу неперервної випадкової величини – перша похідна від функції розподілу цієї величини.

Математичне сподівання неперервної випадкової величини – інтеграл по числовій осі від добутку змінної, якою позначено можливі значення цієї величини, на густину її розподілу.

Відхилення неперервної випадкової величини від її математичного сподівання – різниця між цією величиною та її математичним сподіванням.

Дисперсія неперервної випадкової величини – математичне сподівання квадрата відхилення цієї величини від її математичного сподівання.

Початковий момент s -го порядку випадкової величини (дискретної або неперервної) – математичне сподівання степеня 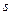цієї величини.

Центральний момент s -го порядку випадкової величини (дискретної або неперервної) – математичне сподівання степеня 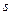відхилення цієї величини від її математичного сподівання.

Асиметрія випадкової величини (дискретної або неперервної) – відношення центрального моменту 3-го порядку до куба середнього квадратичного відхилення цієї величини.

Ексцес випадкової величини (дискретної або неперервної) – відношення центрального моменту 4-го порядку до четвертого степеня середнього квадратичного відхилення цієї величини, зменшене на число три.

п -вимірна випадкова величина – упорядкована сукупність одновимірних випадкових величин, які задані на одному і тому ж просторі елементарних подій.

Закон розподілу двовимірної дискретної випадкової величини – перелік її можливих значень та їх ймовірностей.

Функція розподілу двовимірної випадкової величини (X, Y) – ймовірність сумісної появи подій і .

Густина розподілу ймовірностей двовимірної неперервної випадкової величини – друга мішана похідна від функції розподілу.

Математичне сподівання складової двовимірної дискретної випадкової величини – сума добутків усіх можливих значне відповідної складової на їх імовірності.

Відхилення складової двовимірної випадкової величини від її математичного сподівання – різниця між цією складовою та її математичним сподіванням.

Дисперсія складової двовимірної дискретної випадкової величини – сума добутків квадратів відхилень значень цієї складової від її математичного сподівання на відповідні їм імовірності.

Середнє квадратичне відхилення складової двовимірної випадкової величини – квадратний корінь із дисперсії відповідної складової.

Коваріація (кореляційний момент) двовимірної випадкової величини - математичне сподівання добутку відхилень складових цієї величини від їх математичних сподівань.

Коефіцієнт кореляції двовимірної випадкової величини – відношення коваріації цієї величини до добутку середніх квадратичних відхилень складових цих величин.

Корельовані випадкові величини – дві випадкові величини, коефіцієнт кореляції яких не дорівнює нулю.

Некорельовані випадкові величини – дві випадкові величини, коефіцієнт кореляції яких дорівнює нулю.

Умовна ймовірність складової двовимірної дискретної випадкової величини – імовірність можливих значень однієї складової, обчислена за умови, що друга величина набуває певного можливого значення.

Умовний закон розподілу складової двовимірної дискретної випадкової величини – перелік усіх можливих значень відповідної складової та їх умовних ймовірностей.

Умовне математичне сподівання складової дискретної двовимірної випадкової величини – сума добутків можливих значень відповідної складової на їх умовні ймовірності.

Умовна дисперсія складової двовимірної дискретної випадкової величини – сума добутків квадратів відхилень значень цієї складової від її умовного математичного сподівання на відповідні їм умовні ймовірності.

Густина розподілу складової двовимірної неперервної випадкової величини – інтеграл від двовимірної густини розподілу за змінною, якою позначення значення другої складової.

Умовна густина складової двовимірної неперервної випадкової величини – відношення двовимірної густини розподілу цієї величини до густини розподілу іншої складової.

Умовне математичне сподівання складової двовимірної неперервної випадкової величини – інтеграл від добутку змінної, якою позначені можливі значення відповідної складової, на її умовну густину.

Умовна дисперсія складової двовимірної неперервної випадкової величини – інтеграл від добутку змінної, якою позначені квадрати відхилення значень цієї складової від її умовного математичного сподівання на умовну густину розподілу даної складової.

Стохастична залежність між випадковими величинами – аналітична залежність умовного розподілу однієї з них від значень, яких набуває друга величина.

Функція одного випадкового аргументу – відповідність між можливими значеннями двох одновимірних випадкових величин.

Закон розподілу значень функції одного дискретного аргументу – перелік можливих значень функції та їх ймовірностей.

Функція двох випадкових аргументів – відповідність між парами можливих значень двовимірної випадкової величини і можливими значеннями одновимірної випадкової величини.

Функція двох випадкових аргументів – відповідність між парами можливих значень двовимірної випадкової величини і можливими значеннями одновимірної випадкової величини.

Закон розподілу значень функції двох дискретних випадкових аргументів – перелік можливих значень функції та їх ймовірностей.

Дата добавления: 2015-05-10