Понятия и определения к теме

“Элементы теории графов”

Теория графов широко применяется для анализа функционирования сложных систем, таких как сети железных дорог, авиалиний, телефонных, компьютерных сетей, ирригационных систем. Применяется в автоматизации управления производством, в календарном сетевом и планировании, в экономическом планировании.

Основным понятием теории графов является граф.

Пусть - некоторое непустое множество, 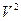- множество всех его двухэлементных подмножеств, 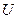- подмножество 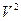. Тогда пара множеств называется неориентированным графом. Элементы множества называются вершинами графа, а элементы множества 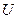ребрами графа.

Неориентированный графG=(S,U) это конечное множество вершин и множество ребер .

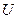Ребро – это неупорядоченная пара вершин графа, между которыми установлена связь. (Замечание: отрезок служит лишь изображением ребра на плоскости).

Дуга – это упорядоченная пара вершин графа, между которыми установлена связь, то есть в паре вершин и 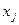указано направление связи – какая из вершин является начальной, а какая конечной.

Ориентированный граф G=(S,U) – это конечное множество вершин и дуг .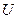

Два ребра называются смежными, если они имеют общий конец.

Две дуги называются смежными, если конец первой дуги является началом второй.

Две вершины называются смежными, если между ними существует связь.

Вершина и ребро (дуга) называются инцидентными, если вершина является концевой вершиной ребра(дуги) , и не инцидентными в противном случае.

Смежность – есть отношение между однородными элементами графа, а инцидентность – есть отношение между разнородными элементами графа.

Порядком графа называется число его вершин.

Степенью P(xi) вершины называется число ребер(дуг) графа, инцидентных данной вершине.

Изолированной называется вершина степени нуль.

Висячей называется вершина степени один.

Петлей называют ребро (дугу) концевые вершины которого совпадают.

Граф G называется простым, если он не содержит петель и параллельных ребер (дуг).

Полным графом называется простой граф, в котором каждая пара вершин смежна.

Псевдографом называется граф, содержащий петли.

Мультиграфом называется граф, содержащий хотя бы две параллельные дуги (ребра).

Число ребер в полном графе равно

Два графа и называются изоморфными, если между множеством их вершин существует такое взаимно-однозначное соответствие, при котором в одном из графов ребрами (дугами) соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.

Способы задания графов:

§ задание множеств и

§ с помощью рисунка (графический)

§ с помощью матрицы(единственный способ задания графа на ЭВМ)

Дата добавления: 2015-05-10