Маршруты, цепи, циклы

Маршрутом, соединяющим вершины 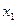и называется чередующаяся последовательность вершин и ребер графа , такая что 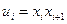, где 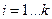. Маршрут можно задать последовательностью его вершин или последовательностью ребер.

Цепью называется маршрут, все ребра которого различны.

Простой цепью называется маршрут, все вершины которого, кроме, возможно, крайних, различны.

Маршрут называется циклическим, если его крайние вершины совпадают.

Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом.

Длиной маршрута называется число ребер в маршруте.

Путь – это ориентированный маршрут.

Неориентированный граф называется связным, а орграф – слабосвязным, если любые две его несовпадающие вершины соединены маршрутом (для орграфа принимать в расчет ориентацию дуг не следует).

Орграф называется сильносвязным, если для любых двух его вершин 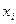и 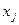найдется путь с началом в 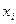и концом в .

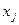Дата добавления: 2015-05-10