Білет №4. Геометричний спосіб визначення рівнодіючої

Геометричний спосіб визначення рівнодіючої

плоскої системи збіжних сил

Теорема. Плоска система збіжних сил у загальному випадку еквіва-лентна рівнодіючій, яка дорівнює векторній сумі цих сил; лінія дії рівно-діючої проходить через точку перетину ліній дії складских.

Нехай дано плоску систему трьох сил Р1,Р2,Р3 лінії дії яких схо­дяться у точці А. За висновками з аксіом III і IV перенесемо ці сили вздовж ліній їх дії у точку А. Додавши сили Р₁ і Р₂ за правилом паралелограма, знайдемо їх рівнодіючу R1

Застосовуючи ту саму аксіому паралелограма, додамо рівнодіючу R1, і силу P3

Скорочено це рівняння запишемо так:

де R — рівнодіюча даної системи трьох сил.

Такі самі міркування можна застосувати де будь-якої кількості збіжних сил, тоді

Обертання навколо нерухомої осі

· Рух. при якому хоча б дві точки твердого тіла чи незмінної системи залишаються нерухомими, називається обер т а л ь н її м; пряма, яка сполучає ці дві точки, називається в і сею об е р т а и н я. В означенні обертального руху йдеться про незмінну систему, тому вісь обертання може бути й за межами тіла.

· Обертальний рух у техніці — явище дуже поширене. Переважна більшість механізмів і машин мають ланки, які рухаються обертально, наприклад вали, зубчасті колеса, кривошипи тощо. Зазначимо, що поняття обертального руху може стосуватися лише тіла, але не точ­ки; так, наприклад, рух точки по колу — не обертальний рух. а криволінійний.

· Розглянемо диск, який обертається навко­ло осі, перпендикулярної до рисунка 10.3. Точка О — слід цієї осі. Очевидно, що траєк­торії точок обертового тіла є кола різних ра­діусів, розміщені в площинах, перпендику­лярних до осі обертання, з центрами, що ле­жать на цій осі.

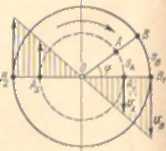
Нехай за час t диск повернувся на кут ф. При цьому точка А пройшла шлях Sa, а точка В — шлях s_fi. Оскільки точки, що містяться на різних відстанях від осі обертання, за той самий проміжок часу проходять різні шляхи, то вони мають різні швидкості і прискорення.

Огже, під час обертального руху тіла його точки, що містяться на різних відстанях від осі обертання, мають неоднакові траєкторії, швидкості і прискорення.

Звідси виходить, що лінійне переміщення (шлях), лінійна швидкість і прискорення не можуть характеризувати обертальний рух тіла в ці­лому. Обертальний рух тіла можна характеризувати кутом <р, на який ВОНО повертається за даний проміжок часу. Цей кут називають кутовим переміщенням тіла. Кутове переміщення виражають у радіанах (рад) або обертах (об); в останньому випадку кутове переміщення позначають Я. Щоб установити залежність між кутом <р і N, складемо пропорцію:

де N — кількість обертів тіла.

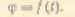
З рис. 10.3 видно, що шлях будь-якої точки обертового тіла

де г — відстань точки від осі обертання. Швидкість будь-якої точки тіла визначається так:

Дата добавления: 2015-05-08