Метрики сложности

Граничный объем

Объем программы

Холстед вводит метрику объема (размера) программы как

В качестве символов используются логические символы (не буквы, а слова целиком)

Потенциальный объем – предельно сжатое представление программы. Он предполагает, что есть язык, в котором в виде процедур реализован любой необходимый алгоритм.

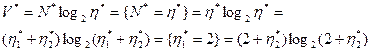
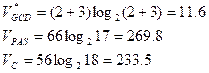
Уровень программы.

- уровень программы

- сложность программы

- оценка уровня программы

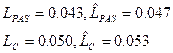
Интеллектуальное содержание (информативность) программы

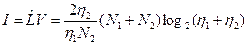
Инвариантно представлению алгоритма на определенном языке.

Еще один способ вычисления Наибольшего Общего Делителя (НОД): все НОД вычислены и хранятся в таблице:

			…
…			НОД(i, j)

GCD:=Table[A,B]

Оператор	Операнд
	,			Table
	:			A
	:=			B
	[]			GCD

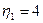
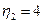
Другая распространенная группа метрик программных проектов – показатели, характеризующие их сложность. Эти метрики используются главным образом для апостериорного анализа, однако могут применяться и на ранних стадиях работы при осуществлении проектирования.

Основная цель метрик сложности – выявить наиболее критичные участки программного проекта, которые являются потенциальными источниками ошибок и повышенных рисков на всех стадиях его жизненного цикла.

Сложность определяется количеством маршрутов.

Метрика позволяет определить:

1) Необходимое число тестов

2) Сложность сопровождения

3) Прогнозируемое число ошибок

Маршруты делятся на:

1) Вычислительные маршруты. На каждом маршруте фиксируются данные и для каждого данного выбираются максимальные, минимальные значения, значения в точках разрыва и 1-2 средних значения. Сложность ,

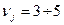
- число вычислительных маршрутов

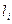- число данных в i-м маршруте

2) Маршруты принятия логических решений. Сложность оценивается числом ветвлний на каждом маршруте.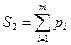

Общая сложность программы ,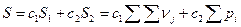

где с₁ и с₂ – весовые коэффициенты, задаваемые в зависимости от назначения программы.

Для оценки структурной сложности при тестировании логики программы вводят упрощенные критерии тестирования, поскольку полное тестирование невозможно.

Критерий 1. Критерий минимального покрытия. Отобранные маршруты должны хотя бы один раз покрывать каждую вершину и каждую дугу графа управления программы. Повторная проверка дуг не требуется.

Пример 1.

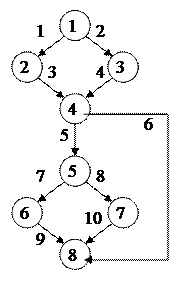
Критерий 1.

М1: 1-2-4-8
М2: 1-2-4-5-6-8
М3: 1-3-4-5-7-8

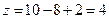
жирным выделены ветвления

Пример 2.

,

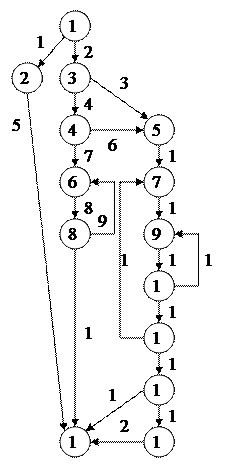
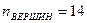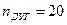
Критерий 1.

М1: 1-2-14
М2: 1-3-4-6-8-6-8-14
М3: 1-3-5-7-9-10-11-12-13-14
М4: 1-3-4-5-7-9-10-9-10-11-7-9-10-11-12-14

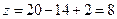
Критерий 2. Отбор базовых маршрутов, оцениваемых по цикломатическому числу графа (число McCabe)

Впервые графическое представление программ было предложено Маккейбом. Основной метрикой сложности он предлагает считать цикломатическую сложность графа программы, или, как ее еще называют, цикломатическое число Маккейба, характеризующее трудоемкость тестирования программы.

Одна из самых распространенных таких метрик – цикломатическая сложность, впервые предложенная Томасом МакКейбом (Thomas McCabe) в 1976 г. Данная метрика предназначена для оценивания сложности потока управления программы (control flow graph) и вычисляется на основе ориентированного графа, где вычислительные операторы или выражения представляются в виде узлов, а передача управления между узлами – в виде дуг.

Формула вычисления цикломатической сложности выглядит следующим образом:

C = e – n + p,

где e – число ребер, n – число узлов, p – число соединенных компонент графа управляющей логики. Упрощенно формулу можно рассматривать как количество ветвлений, которые может проходить программа, увеличенное на единицу.

Метрика цикломатической сложности может быть рассчитана для модуля, метода и других структурных единиц программы.

В процессе анализа значений показателя для отдельных структурных элементов можно выявить элементы с высоким значением показателя (к примеру, нормальное значение показателя для метода – не выше 5–7), что свидетельствует о сложности их управляющей логики и, соответственно, высоких трудозатратах на разработку, тестирование и сопровождение.

Вычисление метрики в ходе реализации проекта (а при детальном проектировании оно возможно еще на этом этапе, не дожидаясь стадии кодирования) позволяет своевременно определить наиболее сложные, сопровождающиеся высокими рисками, структурные единицы и принять меры по устранению рисков за счет внесения коррективов.

В целом, метрики цикломатической сложности являются весьма хорошим способом своевременно зажечь перед разработчиками «красный свет», прекратить дальнейшее усложнение отдельных составляющих проекта и упростить их, предупредив вероятные проблемы с запутанным и нестабильным кодом в будущем.

ЦМЧ: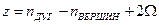

где 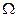- число связных компонент графа, равно числу дуг, необходимых для того, чтобы граф стал максимально связным (граф, в котором любая вершина достижима из любой другой вершины)

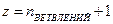(если нет тупиков)

Выбираются все линейно-независимые циклы и линейно-независимые ациклические маршруты. При этом каждый маршрут отличается от остальных хотя бы одной вершиной или дугой.

Для примера 1.

М1: 1 -2- 4 -8

М2: 1 -2- 4 - 5 -6-8

М3: 1 -3- 4 - 5 -7-8

М4: 1 -2- 4 - 5 -7-8

(М5): 1-3-4-8 – возможен, но не включается так как состоит из М1 и М3

(М6): 1-3-4-5-6-8 – возможен, но не включается так как состоит из М2 и М3

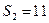
Для примера 2

М1: 6- 8

М2: 9- 10

М3: 7-9- 10 - 11

М1-М3 – линейно-независимые циклические

М4: 1 -2-14

М5: 1 - 3 - 4 -6- 8 -14

М6: 1 - 3 -5-7-9- 10 - 11 - 12 -13-14

М7: 1 - 3 - 4 -5-7-9- 10 - 11 - 12 -13-14

М8: 1 - 3 - 4 -5-7-9- 10 - 11 - 12 -14

М4-М8 – линейно независимые ациклические

S₂=26

жирным – ветвления

Исследование графов реальных программ позволяют сделать замечания:

1) суммарная структурная сложность в основном определяется числом ветвлений и меньшей степени зависит от других структурных компонент графа

2) при фиксированном числе вершин в «широких» графах будет больше маршрутов, но сами маршруты будут короче, и наоборот, «узкие» графы имеют меньшее число, но более продолжительных маршрутов, в результате чего оценка сложности S₂ меняется меньше чем цикломатическое число и больше коррелированна с общим числом графа. Для автоматического анализа графа по второму критерию можно использовать матрицы смежности, в которых элемент a_ij=1 если вершина j достижима из вершины j за одни шаг, и матрицы достижимости, в которых элемент d_ij, если вершина j достижима из i за любое число шагов.

n – число вершин

Основным средством анализа является матрица достижимости, в которой единичные диагональные элементы соответствуют циклам, а одинаковые строки образуют тела соответствующих циклов.

Успешно тестируются программы, у которых Z<=10

Могут тестироваться программы с Z<=30

Для программ с Z>30 успешное тестирование практически невозможно

Критерий 3.

Основанный на выделении полного состава базовых маршрутов выполнения программы. При отборе учитываются все ациклические маршруты и все входящие в них циклические маршруты. При этом для каждого ациклического маршрута должны учитываться все достижимые из них циклы.

Для примера 2.

М1: 1-2-14

М2: 1-3-4-6-8-14

М3: 1-3-4-6-8-6-8-14

М4: 1-3-5-7-9-10-11-112-14

М5: 1-3-5-7-9-10-9-10-11-7-9-10-11-12-14

М6: 1-3-4-5-7-9-10-11-12-13-14

М7: 1-3-4-5-7-9-10-11-7-9-10-11-12-13-14

М8: 1-3-5-7-9-10-11-12-13-14

М9: 1-3-5-7-9-10-11-7-9-10-11-12-13-14

М10: 1-3-4-5-7-9-10-11-12-14

М11: 1-3-4-5-7-9-10-11-7-9-10-11-12-14

S₂=66

Недостаток:

учет только однократного повторения циклов, в действительности при тестировании необходимо проверить минимально возможное повторение циклов, максимальное значение повторения циклов и 1-2 промежуточных значения

Дата добавления: 2015-05-31