Доверительный интервал

Вопрос 47

Доверительным называется интервал, который с заданной надежностью 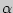покрывает оцениваемый параметр.

Для оценки математического ожидания 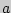случайной величины 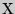, распределенной по нормальному закону, при известном среднем квадратическом отклонении 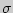служит доверительный интервал

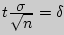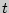где - точность оценки, - объем выборки, - выборочное среднее, - аргумент функции Лапласа, при котором

Пример 166. Найти доверительный интервал для оценки с надежностью 0,9 неизвестного математического ожидания 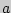нормально распределенного признака 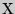генеральной совокупности, если среднее квадратическое отклонение , выборочная средняя и объем выборки .

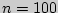Решение. Требуется найти доверительный интервал

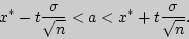
Все величины, кроме 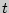, известны. Найдем 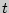из соотношения .

По таблице приложения 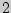находим 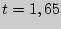и получаем доверительный интервал .

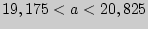Если среднее квадратическое отклонение 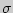неизвестно, то для оценки 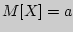служит доверительный интервал

где 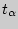находится в приложении 4 по заданным и 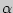, а вместо 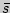часто бывает возможно подставить любую из оценок

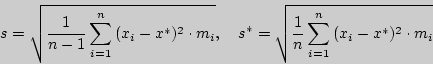
- исправленное среднеквадратическое, статистическое среднеквадратическое отклонения соответственно. При увеличении обе оценк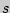и и будут различаться сколь угодно мало и будут сходиться по вероятностям к одной и той же величине .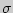

Пример 167. Из генеральной совокупности извлечена выборка объема

= 50:

	-1

Оценить с надежностью 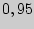математическое ожидание 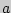нормально распределенного признака генеральной совокупности по выборочной средней.

Решение. Выборочную среднюю и исправленное среднее квадратическое отклонение найдем соответственно по формулам

Пользуясь таблицей приложения 4, по 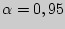и находим .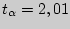

Найдем искомый доверительный интервал:

подставляя , , 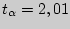, , 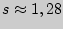получим .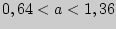

Пример 168. Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города Ярославля представлены в группированном виде:

-	24 - 32	32 - 40	40 - 48	48 - 56	56 - 64	64 - 72	72 - 80

Построить доверительный интервал с надежностью для средней длительности оборотных средств торговых фирм города.

Решение. Найдем выборочную среднюю длительности оборотных средств.

Для упрощения вычисления исправленного среднеквадратического отклонения выберем приближенное значение 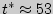. Тогда

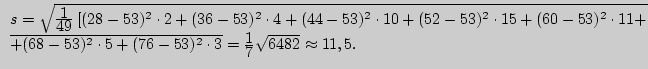
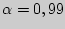В приложении 4 по и находим 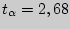, а следовательно, и доверительный интервал

или .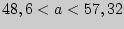

Рассматривая независимых испытаний, можно оценить вероятность 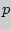по относительной частоте.

Пример 169. Сколько раз надо подбросить монету, чтобы с вероятностью можно было ожидать, что относительная частота появления "герба" отклонится от вероятности этого события по абсолютной величине не более чем на ?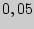

Решение. По условию , , .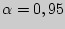

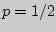Тогда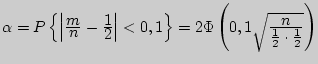

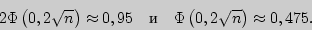
Из таблицы значений функции Лапласа находим, что 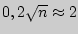, откуда .

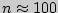Точечные оценки неизвестных параметров распределения можно находить по методу наибольшего правдоподобия, предложенному Р. Фишером.

Пример 170. Найти методом наибольшего правдоподобия оценку параметра 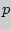биномиального распределения

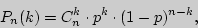
если в независимых испытаниях событие 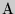появилось раз и в 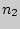независимых испытаниях событие появилось 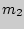раз.

Решение. Составим функцию правдоподобия:

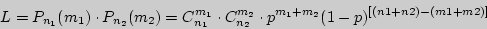
Найдем логарифмическую функцию правдоподобия:

Вычислим первую производную по :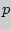

Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:

Решив полученное уравнение относительно 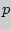, найдем критическую точку:

в которой производная отрицательна. Следовательно, - точка максимума и, значит, ее надо принять в качестве наибольшего правдоподобия неизвестной вероятности 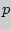биномиального распределения.

Вопросы для самоконтроля

1. Какая оценка называется точечной?

2. Какие точечные оценки генеральных числовых характеристик вы знаете?

3. Чем определяется интервальная оценка?

4. Надежность оценки и другое ее название.

5. На чем основано нахождение доверительного интервала для оценки математического ожидания?

6. Каким образом оценивают истинное значение измеряемой величины?

7. Точечная и интервальная оценка вероятности биномиального распределения.

8. В чем суть метода наибольшего правдоподобия?

Дата добавления: 2015-05-26