
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервальные оценки
|
|
|
|
Задачи
I 331. Игральная кость подбрасывается 300 раз. Какова вероятность того, что относительная частота появления шести очков на верхней грани кости отклонится от вероятности появления события в одном испытании по абсолютной величине не более чем на 0,05?
332. Сколько раз надо подбросить монету, чтобы с вероятностью 0,95 можно было ожидать, что относительная частота появления "герба" отклонится от вероятности этого события по абсолютной величине не более чем на 0,1?
333. Случайная величина 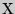 имеет нормальное распределение с известным средним квадратическим отклонением
имеет нормальное распределение с известным средним квадратическим отклонением 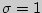 . Найдите доверительные интервалы для оценки неизвестного математического ожидания
. Найдите доверительные интервалы для оценки неизвестного математического ожидания  по выборочным средним
по выборочным средним 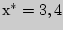 , если объем выборки
, если объем выборки  и задана надежность оценки
и задана надежность оценки 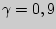 .
.
334. Исследовалось время безотказной работы 50 лазерных принтеров. Из априорных наблюдений известно, что среднее квадратическое отклонение времени безотказной работы  ч. По результатам исследований получено среднее время безотказной работы
ч. По результатам исследований получено среднее время безотказной работы 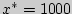 ч. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.
ч. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.
335. Количественный признак 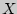 генеральной совокупности распределен нормально. По выборке объема
генеральной совокупности распределен нормально. По выборке объема  найдено "исправленное" среднее квадратическое отклонение
найдено "исправленное" среднее квадратическое отклонение 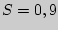 . Найдите доверительный интервал, покрывающий генеральное среднее квадратическое отклонение
. Найдите доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 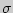 с надежностью
с надежностью 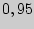 .
.
336. Произведено 16 измерений одним прибором некоторой физической величины, причем исправленное среднее квадратическое отклонение 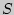 случайных ошибок измерений оказалось равным 0,7. Найдите интервал ошибок прибора с надежностью 0,99. Предполагается, что ошибки измерений распределены нормально.
случайных ошибок измерений оказалось равным 0,7. Найдите интервал ошибок прибора с надежностью 0,99. Предполагается, что ошибки измерений распределены нормально.
II 337. Время (в минутах) обслуживания клиентов в железнодорожной кассе представлено выборкой: 2,0; 1,5; 1,0; 1,0; 1,25; 3,5; 3,0; 3,0; 3.75; 3,7; 4,0; 6,0; 7,0; 1,5; 8,0; 3,5; 5,0; 3,5; 14,0; 12,0; 15,1; 18,0; 18,5; 17,0. Определите процент клиентов, время обслуживания которых более 12 минут и менее 5 минут.
338. Из генеральной совокупности извлечена выборка объема  :
:
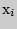
| -0,4 | -0,2 | -0,1 | 0,2 | 0,5 | 0,7 | 1,2 | 1,6 | ||

|
Оцените с надежностью 0,9 математическое ожидание 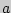 нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
III 339. Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:
| 24-33 | 33-42 | 42-51 | 51-60 | 60-69 | 69-78 | 78-87 |

|
Постройте доверительный интервал с надежностью 0,95 для средней длительности оборотных средств торговых фирм города при условии, что среднее квадратическое отклонение 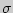 неизвестно (известно и равно 10 дням).
неизвестно (известно и равно 10 дням).
340. Найти методом наибольшего правдоподобия оценку параметра 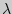 распределения Пуассона
распределения Пуассона
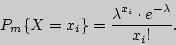
В п.1 и п.2 мы рассмотрели вопрос об оценке неизвестного параметра a одним числом. Такая оценка называется точечной. В ряде случаев требуется не только найти для параметра а подходящее численное значение, но и оценить его надежность и точность. Требуется знать - к каким ошибкам может привести замена параметра а его точечной оценкой, и с какой уверенностью можно ожидать, что ошибки не выйдут за известные пределы. Чтобы дать представление о точности и надежности оценки 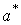 , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
Рассмотрим в качестве примера задачу о доверительном интервале при оценке математического ожидания.
Пусть для параметра а получена из ряда экспериментов несмещенная оценка 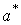 . Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность
. Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность  (например,
(например, 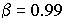 ), такую, что событие с вероятностью
), такую, что событие с вероятностью  можно считать практически достоверным, и найдем такое значение e, для которого
можно считать практически достоверным, и найдем такое значение e, для которого
P (| 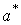 - a | < e) = - a | < e) = 
| (8) |
Тогда диапазон практически наиболее вероятных значений ошибки, возникающих при замене a на 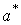 , по модулю не будет превосходить е. Большие по абсолютной величине ошибки будут появляться с малой вероятностью
, по модулю не будет превосходить е. Большие по абсолютной величине ошибки будут появляться с малой вероятностью 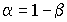 .
.
Равенство (8) означает, что с вероятностью  неизвестное значение параметра а попадает в интервал
неизвестное значение параметра а попадает в интервал
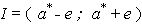 .
.
Необходимо отметить следующее обстоятельство. Ранее мы рассматривали близость случайной оценки к истинному значению оцениваемого параметра. Здесь ситуация несколько другая. Величина а не случайна, зато случаен интервал I. И величину  можно трактовать как вероятность того, что случайный интервал I накроет истинное значение параметра а. Вероятность
можно трактовать как вероятность того, что случайный интервал I накроет истинное значение параметра а. Вероятность  называется доверительной вероятностью, I - доверительным интервалом, а
называется доверительной вероятностью, I - доверительным интервалом, а
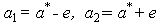
называются доверительными границами. Перейдем теперь к нахождению доверительных границ 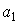 и
и 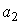 . Пусть для параметра а существует несмещенная оценка
. Пусть для параметра а существует несмещенная оценка 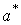 . Если бы нам была известна функция распределения случайной величины (или плотность распределения вероятности)
. Если бы нам была известна функция распределения случайной величины (или плотность распределения вероятности) 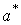 , то задача нахождения доверительнего интервала была бы весьма проста: достаточно было бы найти такое значение e, для которого выполняется условие (8). Затруднение состоит в том, что функция распределения оценки
, то задача нахождения доверительнего интервала была бы весьма проста: достаточно было бы найти такое значение e, для которого выполняется условие (8). Затруднение состоит в том, что функция распределения оценки 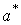 зависит от функции распределения величины Х и, следовательно, от самого неизвестного параметра а.
зависит от функции распределения величины Х и, следовательно, от самого неизвестного параметра а.
В качестве другого примера рассмотрим задачу о доверительном интервале для математического ожидания.
Пусть произведено N независимых опытов над случайной величиной Х, характеристики которой (дисперсия D и математическое ожидание m) неизвестны. Для этих параметров получены оценки:
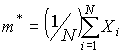 ,
, 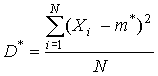 .
.
Требуется построить доверительный интервал I, соответствующий доверительной вероятности  для математического ожидания m величины Х.
для математического ожидания m величины Х.
При решении этой задачи воспользуемся тем, что величина 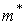 представляет собой сумму N независимых случайных величин
представляет собой сумму N независимых случайных величин 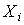 , и, согласно центральной предельной теореме, при достаточно большом N ее закон близок к нормальному. Поэтому будем исходить из того, что величина
, и, согласно центральной предельной теореме, при достаточно большом N ее закон близок к нормальному. Поэтому будем исходить из того, что величина 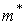 распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно m и D/N. Найдем такую величину е, для которой
распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно m и D/N. Найдем такую величину е, для которой
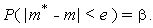
| (9) |
Для нормальной случайной величины (с нулевым математическим ожиданием и единичной дисперсией) функция распределения вероятности

С учетом этого формулу (9) запишем в виде:
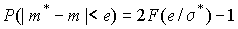
где 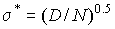 - среднее квадратическое отклонение оценки.
- среднее квадратическое отклонение оценки.
Из уравнения
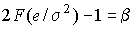
находим значение е:
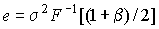
| (10) |
где 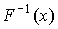 - функция, обратная F(…), т.е. такое значение аргумента, при котором нормальная функция распределения равна х.
- функция, обратная F(…), т.е. такое значение аргумента, при котором нормальная функция распределения равна х.
Дисперсия D, через которую выражена величина 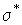 , нам в точности неизвестна. В качестве ее ориентировочного значения можно воспользоваться оценкой
, нам в точности неизвестна. В качестве ее ориентировочного значения можно воспользоваться оценкой 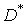 или
или 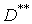 и положить приближенно
и положить приближенно
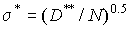 .
.
Таким образом, решена задача построения доверительного интервала
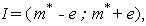
где е определяется формулой (10).
Для удобства в табл. 1 приведены значения величины 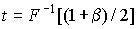 .
.

| t | 
| t | 
| t | 
| t |
| 0.8 | 1.282 | 0.86 | 1.175 | 0.91 | 1.694 | 0.97 | 2.169 |
| 0.81 | 1.310 | 0.87 | 1.513 | 0.92 | 1.750 | 0.98 | 2.325 |
| 0.82 | 1.340 | 0.88 | 1.554 | 0.93 | 1.810 | 0.99 | 2.576 |
| 0.83 | 1.371 | 0.89 | 1.597 | 0.94 | 1.880 | 0.9973 | 3.000 |
| 0.84 | 1.404 | 0.9 | 1.643 | 0.95 | 1.960 | 0.999 | 3.290 |
| 0.85 | 1.439 |
Пример. Пусть в результате проведения 30 опытов были получены 30 значений случайной величины Х:
10.5, 10.8, 11.2, 10.9, 10.6, 11.0, 10.8, 11.0, 11.6, 10.9, 10.5, 11.8, 10.2, 9.2, 10.2, 11.2, 10.3, 11.1, 11.8, 10.3, 10.7, 10.8, 11.2, 10.9, 10.1, 11.7, 10.8, 11.3, 11.0, 11.9.
Требуется найти оценку 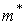 для математического ожидания m величины X и построить доверительный интервал, соответствующий доверительной вероятности
для математического ожидания m величины X и построить доверительный интервал, соответствующий доверительной вероятности 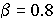 .
.
Вычисляем 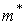 = 10.87,
= 10.87, 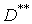 = 0.49. Далее
= 0.49. Далее 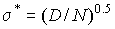 = 0.12.
= 0.12.
По табл. 1 находим: 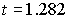 .
.
Тогда
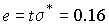 ;
;
доверительные границы:
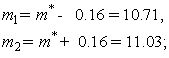
доверительный интервал:
I = (10.71; 11.03).
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 1505; Нарушение авторских прав?; Мы поможем в написании вашей работы!