Виды средних величин

Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая.

В изучении средних величин применяются следующие показатели и обозначения.

Признак, по которому находится средняя, называется осредняемым признаком и обозначается х; величина осредняемого признака у любой единицы статистической совокупности называют индивидуальным его значением, или вариантами, и обозначают как хл, х2, x3,… х_n; частота – это повторяемость индивидуальных значений признака, обозначается буквой f.

В статистике применяют два класса средних: степенные (аналитические) и структурные. Последние используются для характеристики структуры вариационного ряда.

Один из наиболее распространенных видов средней – средняя арифметическая, которая исчисляется тогда, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

Индивидуальные формулы для вычисления средних можно привести к общему виду: ,

где 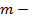показатель степенной средней: при получаем формулу для вычисления средней арифметической, при - средней геометрической, - средней гармонической, при 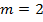- средней квадратической;

- варианты (значения, которые принимает признак);

частоты.

Главным условием, при котором можно использовать степенные средние в статистическом анализе, является однородность совокупности, которая не должна содержать исходных данных, резко различающихся по своему количественному значению (в литературе они носят название аномальных наблюдений).

Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.

Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной.

Средняя арифметическая простая используется в тех случаях, когда данные не сгруппированы или сгруппированы, но все частоты равны между собой.

Если ряд представлен в виде интервального ряда ряспределения, тогда при расчете средней в качестве берут середины интервалов.

Средняя гармоническая величина является модифицированной формой средней арифметической. Она применяется в тех случаях, когда неизвестны значения частот у вариантов ряда, зато имеются для каждого произведения этих вариант на соответствующие им частоты.

Средняя гармоническая

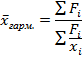
Средняя геометрическая используется для расчета среднего коэффициента или темпа роста статистического показателя.

Для несгруппированных данных с равными частотами применяется средняя геометрическая взвешенная

Для сгруппированных данных с неравными частотами приеняется средняя гармоническая взвешенная

Средняя квадратическая величина широко применяется при оценке вариации признака, при изучении взаимосвязи явлений.

Кроме того, прикладное значение имеет расчет степенных средних и более высоких порядков, например при изучении характеристик распределения случайных величин.

Правило мажорантности в статистике:

Тема 5.3. Показатели вариации в статистике.

Вариацией называется различие значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Колебания отдельных значений характеризуют показатели вариации.

Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака .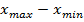

Среднее линейное отклонение () – представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитываются невзвешенное среднее линейное отклонение.

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейной отклонений, где весами выступают частоты соответствующих вариант:

Дисперсией (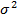) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней:

Для несгруппированных данных: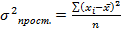

Для сгруппированных данных:

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением)

Для несгруппированных данных:

Для сгруппированным данных: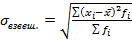

Для сравнения вариаций одного и того же показателя в разных совокупностях (например, заработной платы двух фирм) или вариации различных показателей в одной совокупности (например, вариации заработной платы и возраста внутри одной фирмы) используют относительные показатели вариации. К ним относят:

Коэффициент осцилляции: ;

Относительное линейное отклонение: ;

Коэффициент вариации: ;

Принято считать, что если значение коэффициента вариации больше 33%, то совокупность неоднородна и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во вех видах статистического анализа).

Дата добавления: 2015-05-26